By Jingqi Tian, AliSQL kernel developer.
In the article Analysis of MySQL Cost Estimator, bool JOIN::estimate_rowcount() is analyzed. This function primarily deals with the cost estimation algorithms for various single-table Access Paths. When there is no need for joining multiple tables, the content covered in the previous article essentially constitutes a complete cost estimation.
However, if multiple tables are joined, you must determine the order in which the tables are joined. Different join orders may affect the Access Paths of tables. The process of generating the final physical execution plan is also the process of determining the Access Paths of each table.
Let's start with an example by creating two simple tables and executing a statement to join two tables:
CREATE TABLE t1 (
id INT PRIMARY KEY,
col1 INT, col2 INT,
KEY index_col1 (col1)) ENGINE=INNODB;
CREATE TABLE t2 (
id INT PRIMARY KEY,
col1 INT, col2 INT,
KEY index_col1 (col1)) ENGINE=INNODB;
SELECT t1.*, t2.* FROM t1, t2
WHERE t1.col1 = t2.col2 AND t2.col2 < 10;Even with this simple SQL statement, many Access Paths can be generated.
The optimizer first generates Access Paths for a single table, and then begins to decide on the Join Order. Let's take a look at the Access Path selection for the above SELECT statement under different Join Orders:
When reading table t1 first, the available filter condition is t1.col1 < 10 (since t2.col2 < 10 and t1.col1 = t2.col2). For table t1, the available Access Paths are:
• Full Table Scan
• Index Range Scan using t1.col1 < 10 on index_col1
Next, when reading table t2, since there is no index on col2, only a full table scan can be performed. In MySQL-8.0, Hash Join is implemented, so in this case, a Hash Join method will be used to achieve Inner Join.
• Build a hash table from the records obtained from t1, then perform a full table scan on t2, and probe the read records.
When reading table t2 first, due to the lack of indexes on col2, only a full table scan can be performed, filtering for records where t2.col2 < 10.
Next, when reading table t1, the available Access Paths are:
• Perform a full table scan for a Hash Join, comparing the scanned data row by row with the data previously read from t2.
• Use t1.col1 < 10 to perform an Index Range Scan on index_col1 for a Hash Join, comparing the obtained data row by row with the data read from t2, and if a match is found, perform a lookup to get the complete data from t1.
• Use the data read from t2 to search on t1 based on t2.col2 via index_col1; if matching rows are found, perform a lookup to get the complete data from t1.
• If there are ten thousand records in t2 that satisfy t2.col2 < 10, but no records in t1 satisfy t1.col1 < 10, then reading t1 before t2 would be the fastest.
• If there is only one record in t2 that satisfies t2.col2 < 10 and t2 is a small table, while there are many records in t1 that satisfy t1.col1 < 10, but very few records satisfy t1.col1 = t2.col2, then reading t1 before t2 would be very time-consuming, and it would be better to read t2 first.
Based on the above analysis, we have the following findings:
• The data in the table greatly affects the selection of the Join Order.
• In the above two examples, it is better to read the table with fewer records first. In fact, this is what we commonly refer to as using the smaller table as the driving table. Therefore, estimating how much data will be read from a table is crucial, as it greatly influences the Join Order.
• When reading t2 first and then t1, there is actually one additional Access Path: using the data read from the preceding table to search on the current table using an index. Thus, the Access Paths for reading the second table can be categorized into two types:
• scan/range: Similar to the Access Path in the bool JOIN::estimate_rowcount() function discussed in the previous article. If this type of Access Path is used, the corresponding Join algorithm is actually a Hash Join.
• ref/eq_ref: An Access Path that appears only in multi-table joins, involving using records read from the preceding table to search on the indexes of the current table. The corresponding Join algorithm is actually an Index Nested-loop Join.
In MySQL, the basic approach to determining the Join Order can be summarized as enumeration plus cost estimation. Therefore, in this article, we mainly address the following questions:
• How can we enumerate different Join Orders?
• How can we calculate the cost for each Join Order?
• How can we prune during the enumeration process to speed up the operation?
Let's first look at this question: when joining n tables, how many different ways can these joins be performed? We assume that all joins are Inner Joins.
Search Space for Join ReorderLet's first consider joining three tables A, B, and C:
(A⋈B)⋈C, (B⋈A)⋈C, (A⋈C)⋈B, (C⋈A)⋈B, (B⋈C)⋈A, (C⋈B)⋈A
A⋈(B⋈C), A⋈(C⋈B), B⋈(A⋈C), B⋈(C⋈A), C⋈(A⋈B), C⋈(B⋈A)
There are a total of 12 different orders. If you use a formula to express joining n tables, there are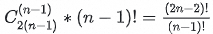 
orders.
When n=4, there are 120 ways to join.
When n=5, there are 1,680 ways to join.
When n=6, there are 30,240 ways to join.
...
Finding the perfect join order for multiple tables is an NP-hard problem, meaning that no algorithm with polynomial complexity can solve it. Traversing all possible Join Orders would result in extremely high algorithm complexity. Therefore, the database optimizer must limit the search space for Join Reorder. This helps find a near-optimal Join Order within a smaller search space.
In MySQL, not all Join Orders are enumerated. MySQL always selects two tables to join first, and then uses the result as the driving table to join with the third table. Therefore, MySQL only needs to calculate the cost for up to n! Join methods. If represented as a tree, all Join Orders searched by MySQL would have a similar structure. Take ((A⋈B)⋈C)⋈D as an example:
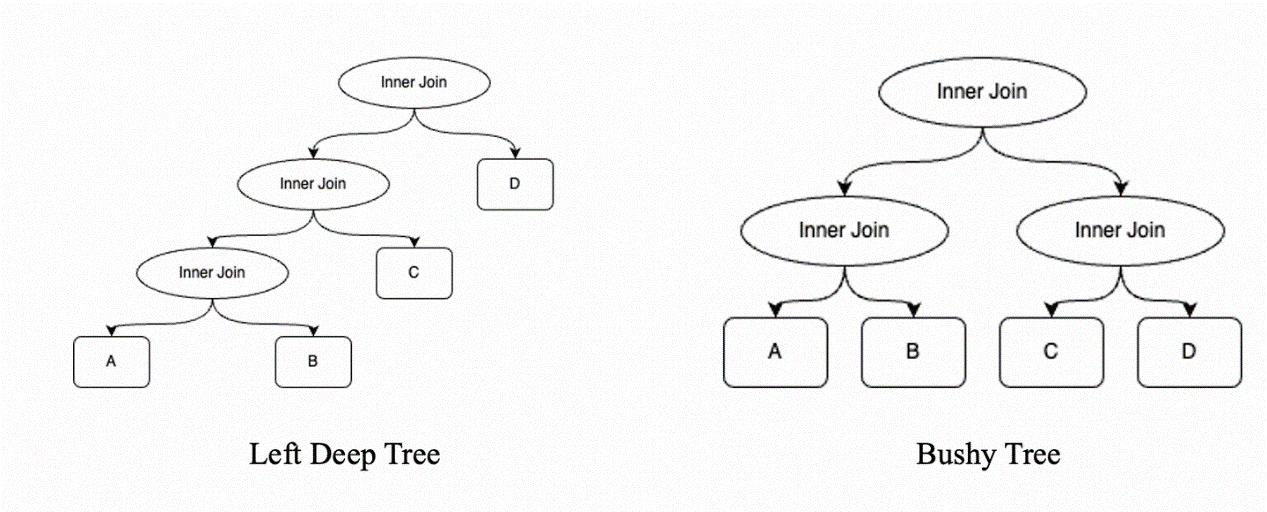
This tree extends unidirectionally to the left, with the right node of each Inner Join always being a single table. Such a tree is called a Left Deep Tree. The complete Join Order space also includes the Bushy Tree shown in the figure, but MySQL never searches for such Join Orders.
As mentioned in the previous section, MySQL only searches for Join Orders that form the left deep tree. However, even for left deep trees, there are n! possibilities, and factorial complexity is still unacceptable. Therefore, MySQL uses the optimizer_search_depth parameter to further control the search space for Join Orders. Let's first discuss the role of the optimizer_search_depth parameter. Suppose we have 10 tables to join, but optimizer_search_depth is set to 3. The search process would work as follows:
The first search determines the first table to join in the complete execution plan. The determination method is to select 3 tables out of the 10 tables and perform a full permutation, calculating the cost for each permutation. The permutation with the lowest cost determines the first table in the complete Join Order.
The second search determines the second table to join in the complete execution plan. The determination method is to select 3 tables out of the remaining 9 tables and perform a full permutation, calculating the cost for each permutation (the cost here is that of the complete plan that includes the first table). The permutation with the lowest cost determines the second table to join in the complete execution plan.
The seventh search determines the seventh table to join in the complete execution plan. The determination method is to select 3 tables out of the remaining 4 tables and perform a full permutation, calculating the cost for each permutation (the cost here is that of the complete plan that includes the first six tables). The permutation with the lowest cost determines the seventh table to join in the complete execution plan.
The eighth search determines the last three tables to join in the complete execution plan. Since only three tables remain, calculate the full permutation of these 3 tables (the cost here is that of the complete plan that includes the first seven tables). The permutation with the lowest cost is added to the complete execution plan.
Here is the pseudocode representation:
procedure greedy_search
input: remaining_tables
output: pplan;
{
pplan =<>; // Partial query plan
do {
// Get the next table t to join and its position n.
(t, n) = best_extension(pplan, remaining_tables);
// Concatenate t with the partial query plan; t is the nth table to join.
pplan = concat(pplan, (t, n));
// Maintain the remaining tables that are not joined.
remaining_tables = remaining_tables - t;
} while (remaining_tables != {
})
return pplan;
}Now, let's calculate the algorithm complexity:
• The first search requires selecting 3 tables out of 10 tables for a full permutation, which has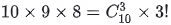 
ways.
• The second search ha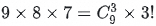s 
ways.
• ...
• The last search ha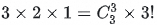s 
ways.
Therefore, summing these up gives:
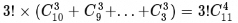
So, if there are N tables to join and the optimizer_search_depth is set to d, the algorithm complexity is:
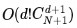
When d≥N, the algorithm complexity is equivalent to enumerating all left deep trees, which is O(N!).
The official MySQL code estimates the algorithm complexity as
. The exact method for calculating this complexity is not clear. If anyone has any insights, feel free to discuss them with us.
The code that decides the Join Order is in the bool Optimize_table_order::choose_table_order() function. The code structure and comments are relatively clear, so those interested can directly view the source code. Here, I will provide a brief introduction.
In MySQL, the default value of optimizer_search_depth is 62, meaning that in most cases, the algorithm complexity will be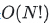 
. Therefore, pruning often plays a more significant role in reducing algorithm execution time (the pruning algorithm will be discussed later).
To make pruning more effective, it is crucial to find a better Join Order as early as possible.
From the example in the introduction, we observe that generally, it is better to read the table with fewer rows first, followed by the table with more rows. This can lead to a better Join Order. If we start by enumerating Join Orders that read smaller tables first, we are more likely to find a better Join Order early on.
Therefore, an important step before selecting the order is pre-sorting. This function sorts the tables based on the following criteria: whether there are dependencies of Outer Join or Straight Join, whether there are key references, and the estimated number of rows from estimate_rowcount():
bool Join_tab_compare_default::operator()(const JOIN_TAB *jt1,
const JOIN_TAB *jt2) const {
// Sorting distinct tables, so a table should not be compared with itself
assert(jt1 != jt2);
// Outer Join and Straight Join enforce a specific join order, so the function first checks if there are any dependencies of Outer Join or Straight Join between tables.
if (jt1->dependent & jt2->table_ref->map()) return false;
if (jt2->dependent & jt1->table_ref->map()) return true;
// The function checks if there are any key dependencies between two tables. For example, if the join condition between t1 and t2 is t1.no_key = t2.key, then t1 should be read first.
const bool jt1_keydep_jt2 = jt1->key_dependent & jt2->table_ref->map();
const bool jt2_keydep_jt1 = jt2->key_dependent & jt1->table_ref->map();
if (jt1_keydep_jt2 && !jt2_keydep_jt1) return false;
if (jt2_keydep_jt1 && !jt1_keydep_jt2) return true;
// If none of the above conditions are met, the function compares the estimated number of rows obtained from the estimate_rowcount() function, placing the smaller table first.
if (jt1->found_records > jt2->found_records) return false;
if (jt1->found_records < jt2->found_records) return true;
return jt1 < jt2;
}Then it moves into the bool Optimize_table_order::greedy_search(table_map remaining_tables) function.
The pseudocode for greedy_search() is already presented in the section on the Join Reorder search algorithm. Below, the author outlines the main logic of the actual MySQL source code. Interested readers can take a look at it:
bool Optimize_table_order::greedy_search(table_map remaining_tables) {
// const_tables does not participate in the join
uint idx = join->const_tables; // index into 'join->best_ref'
// Current best_idx that is searched
uint best_idx;
POSITION best_pos;
JOIN_TAB *best_table; // the next plan node to be added to the curr QEP
DBUG_TRACE;
/* Number of tables that we are optimizing */
// remaining_tables is a bitmap that calculates the number of tables to be optimized
const uint n_tables = my_count_bits(remaining_tables);
/* Number of tables remaining to be optimized */
uint size_remain = n_tables;
...
// Start the loop to execute the search process described in the Join Reorder search algorithm
do {
/* Find the extension of the current QEP with the lowest cost */
// Cost estimation for the current best complete query plan
join->best_read = DBL_MAX;
// Rowcount for the current best complete query plan
join->best_rowcount = HA_POS_ERROR;
found_plan_with_allowed_sj = false;
// Start the first search; tables from 0 to idx-1 are const_tables and do not participate in the search, so we start from the idx-th table
// Set the search depth to search_depth
if (best_extension_by_limited_search(remaining_tables, idx, search_depth))
return true;
/*
'best_read < DBL_MAX' means that optimizer managed to find
some plan and updated 'best_positions' array accordingly.
*/
assert(join->best_read < DBL_MAX);
// If the number of remaining tables to be optimized is less than or equal to search_depth, it means this is the last search and we can finish
if (size_remain <= search_depth || use_best_so_far) {
/*
'join->best_positions' contains a complete optimal extension of the
current partial QEP.
*/
DBUG_EXECUTE(
"opt",
print_plan(join, n_tables,
idx ? join->best_positions[idx - 1].prefix_rowcount : 1.0,
idx ? join->best_positions[idx - 1].prefix_cost : 0.0,
idx ? join->best_positions[idx - 1].prefix_cost : 0.0,
"optimal"););
return false;
}
/* select the first table in the optimal extension as most promising */
// join->best_positions[idx] records the first table in the current search with the lowest cost, which is the table we want
best_pos = join->best_positions[idx];
best_table = best_pos.table;
/*
Each subsequent loop of 'best_extension_by_limited_search' uses
'join->positions' for cost estimates, therefore we have to update its
value.
*/
// join->positions maintains the current search status
join->positions[idx] = best_pos;
...
/* find the position of 'best_table' in 'join->best_ref' */
// Maintain best_ref, which is the current optimal query plan
best_idx = idx;
JOIN_TAB *pos = join->best_ref[best_idx];
while (pos && best_table != pos) pos = join->best_ref[++best_idx];
memmove(join->best_ref + idx + 1, join->best_ref + idx,
sizeof(JOIN_TAB *) * (best_idx - idx));
join->best_ref[idx] = best_table;
// Maintain remaining_tables
remaining_tables &= ~(best_table->table_ref->map());
...
// The number of remaining tables to be optimized is decremented by one.
--size_remain;
// The index for the table to be determined for the join next time is incremented by one.
++idx;
} while (true);
}The greedy_search() function calls the best_extension_by_limited_search() function, which performs a search of optimizer_search_depth to determine the next table to join.
The principle behind this function is simple: it works by selecting and arranging optimizer_search_depth tables from the remaining tables, and calculating the cost. The source code of the best_extension() function is similar to its pseudocode, so here we only present the pseudocode.
Pseudocode:
procedure best_extension_by_limited_search(
pplan in, // in, partial plan of tables-joined-so-far
pplan_cost, // in, cost of pplan
remaining_tables, // in, set of tables not referenced in pplan
best_plan_so_far, // in/out, best plan found so far
best_plan_so_far_cost,// in/out, cost of best_plan_so_far
search_depth) // in, maximum size of the plans being considered
{
for each table T from remaining_tables
{
// Calculate the cost of using table T as above
// For each table to be optimized, perform a series of complex cost calculations
cost = complex-series-of-calculations;
// Add the cost to the cost so far.
// Add cost to pplan_cost
pplan_cost+= cost;
// Pruning
prune_by_cost
pruned_by_heuristic
// Extend the current pplan with the best_access_method obtained above
pplan= expand pplan by best_access_method;
remaining_tables= remaining_tables - table T;
// If there are tables that are not joined and search_depth is greater than 1
if (remaining_tables is not an empty set
and
search_depth > 1)
{
// If table T is optimized by EQ_REF-joined, extend it with eq_ref_eq_ref_extension_by_limited_search
// Otherwise, extend it with best_extension_by_limited_search
if (table T is EQ_REF-joined)
eq_ref_eq_ref_extension_by_limited_search(
pplan, pplan_cost,
remaining_tables,
best_plan_so_far,
best_plan_so_far_cost,
search_depth - 1);
else
best_extension_by_limited_search(pplan, pplan_cost,
remaining_tables,
best_plan_so_far,
best_plan_so_far_cost,
search_depth - 1);
}
else
{
// Maintain the cost of the best plan found so far
best_plan_so_far_cost= pplan_cost;
best_plan_so_far= pplan;
}
}
}The cost calculation methods and pruning techniques used in this function will be detailed in later sections.
There is a special optimization in this function. If the current table being joined uses the eq_ref method (where eq_ref refers to joining through a unique key lookup on the driven table), other tables that can also use EQ_REF to join are added to the query plan. This optimization is performed only when a table is joined by using eq_ref for the first time.
In this section, we will look at the cost calculation for a complete multi-table join execution plan.
In the MySQL source code, Access Paths are categorized by the access_type, which includes ref, eq_ref, range, scan, and others. In the cost calculation for Join Reorder, these access_type values are further divided into two categories:
• ref, eq_ref: When the driven table uses this Access Path, the corresponding Join algorithm is Index Nested Loop Join.
• range, scan, and others: When the driven table uses this Access Path, the corresponding Join algorithm is Hash Join.
Before talking about the cost of ref and eq_ref, let's introduce a concept: fanout. Fanout is the number of rows in the driven table that can successfully join with each row in the driving table.
• In terms of eq_ref, for each row in the driving table, there is exactly one row in the driven table that satisfies the join condition. Therefore, the fanout is 1.
• In terms of ref, for each row in the driving table, there can be multiple rows in the driven table that satisfy the join condition. How do we estimate this value? Readers familiar with previous articles will quickly realize that this is essentially the records_per_key statistic, also known as Cardinality.
In this way, we get fanout for both ref and eq_ref. With the fanout for both ref and eq_ref, the IO cost calculation becomes simple. Essentially, it involves multiple index reads, with each read fetching fanout rows. The number of index reads is equal to the number of rows in the driving table (recorded as prefix_rowcount).
During the join process, each row must be processed, so the CPU cost is calculated as:
prefix_rowcount * fanout * row_evaluate_costSummary
Total cost
prefix_rowcount * single_io_cost + prefix_rowcount * fanout * row_evaluate_costPreviously, in the bool JOIN::estimate_rowcount() function, we calculated the costs for various types of Access Paths. Here, we select the Access Path with the smallest cost.
For IO cost, we need to calculate how many times the driven table is read. In MySQL 8.0, although the join algorithm has been upgraded from Block Nested Loop Join to Hash Join, the cost calculation method remains unchanged, still following the Block Nested Loop Join algorithm. Therefore, the number of times the driven table is read is the size of data in the driving table divided by the size of the Join Buffer. The total IO cost is:
To calculate CPU cost, we need to determine the fanout value. The data read from the driven table is not all directly joined; some of it may be filtered by predicates. The impact of this filtering is calculated using the calculate_condition_filter() function, which we won't delve into here. Assume that after filtering, we obtain rows_after_filtering rows of data. Only these rows_after_filtering rows will participate in the join, while others will be filtered out during predicate evaluation and will not be involved in the join computation. Therefore, CPU cost can be divided into two parts:
join_buffer_cnt * (total_records - rows_after_filtering) * row_evalute_cost + prefix_rowcount * rows_after_filtering * row_evalute_costAs a side note, while reading the code, the author noticed that when the Access Path of the driven table is range, the IO cost is directly calculated without considering the Join Buffer. This was quite puzzling, but then the author found the following comment in the MySQL code:
TODO:
We take into account possible use of join cache for ALL/index
access (see first else-branch below), but we don't take it into
account here for range/index_merge access. Find out why this is so.
The comment suggests that while we consider the impact of the Join Buffer when calculating the cost for full table scans or index scans, we do not do so for index range scans. The reason for this discrepancy is currently unknown, and it has been marked as a TODO item for further investigation.
Summary
Total cost
Join_buffer_cnt * single_io_cost + join_buffer_cnt * (total_records - rows_after_filtering) * row_evalute_cost + prefix_rowcount * rows_after_filtering * row_evalute_costFinally, let's look at the row count after the join. For scan and range Access Paths, since the impact of predicates has already been estimated, the row count is. For ref and eq_ref, the impact of other predicates has not yet been considered, so the calculate_condition_filter() function is used again to compute the filter_effect. Therefore, the row count is.
After calculating the cost for ref/eq_ref and scan/range Access Paths, the one with the smallest cost is chosen as the final Access Path for the current table.
if (position->prefix_cost >= join->best_read &&
found_plan_with_allowed_sj) {
DBUG_EXECUTE("opt",
print_plan(join, idx + 1, position->prefix_rowcount,
position->read_cost, position->prefix_cost,
"prune_by_cost"););
trace_one_table.add("pruned_by_cost", true);
backout_nj_state(remaining_tables, s);
continue;
}Cost-based pruning is the simplest. If the current cost is already greater than the smallest cost found so far, pruning is performed directly.
if (prune_level == 1) {
if (best_rowcount > position->prefix_rowcount ||
best_cost > position->prefix_cost ||
(idx == join->const_tables && // 's' is the first table in the QEP
s->table() == join->sort_by_table)) {
if (best_rowcount >= position->prefix_rowcount &&
best_cost >= position->prefix_cost &&
/* TODO: What is the reasoning behind this condition? */
(!(s->key_dependent & remaining_tables) ||
position->rows_fetched < 2.0)) {
best_rowcount = position->prefix_rowcount;
best_cost = position->prefix_cost;
}
} else if (found_plan_with_allowed_sj) {
DBUG_EXECUTE("opt",
print_plan(join, idx + 1, position->prefix_rowcount,
position->read_cost, position->prefix_cost,
"pruned_by_heuristic"););
trace_one_table.add("pruned_by_heuristic", true);
backout_nj_state(remaining_tables, s);
continue;
}
}Heuristic pruning can be enabled or disabled using the optimizer_prune_level parameter. This pruning has a significant impact. If a better partial query plan (with lower row count and cost) is found at the current search depth, the search for the current branch is stopped. In practice, most query plans are pruned by this rule. Without this rule, MySQL would perform an exhaustive search with the default optimizer_search_depth of 62, but with the rule enabled, most query plans are pruned early.
This pruning mainly occurs when a ref or eq_ref Access Path is found, there are several heuristic rules that prevent MySQL from calculating the cost for range or scan Access Paths. There are many rules for this part, and detailed explanations can be found in the MySQL comments.
We do not consider index/table scan or range access if:
1a) The best 'ref' access produces fewer records than a table scan
(or index scan, or range access), and
1b) The best 'ref' executed for all partial row combinations, is
cheaper than a single scan. The rationale for comparing
COST(ref_per_partial_row) * E(#partial_rows)
vs
COST(single_scan)
is that if join buffering is used for the scan, then scan will
not be performed E(#partial_rows) times, but
E(#partial_rows)/E(#partial_rows_fit_in_buffer). At this point
in best_access_path() we don't know this ratio, but it is
somewhere between 1 and E(#partial_rows). To avoid
overestimating the total cost of scanning, the heuristic used
here has to assume that the ratio is 1. A more fine-grained
cost comparison will be done later in this function.
(2) The best way to perform table or index scan is to use 'range' access
using index IDX. If it is a 'tight range' scan (i.e not a loose index
scan' or 'index merge'), then ref access on the same index will
perform equal or better if ref access can use the same or more number
of key parts.
(3) See above note about InnoDB.
(4) NOT ("FORCE INDEX(...)" is used for table and there is 'ref' access
path, but there is no quick select)
If the condition in the above brackets holds, then the only possible
"table scan" access method is ALL/index (there is no quick select).
Since we have a 'ref' access path, and FORCE INDEX instructs us to
choose it over ALL/index, there is no need to consider a full table
scan.This article provides a brief analysis of the process of the MySQL Join Reorder algorithm, including cost calculation and pruning algorithms, with the aim of helping readers understand the specific procedures by which the MySQL optimizer generates execution plans. While reviewing the MySQL optimizer code, the author noticed that many parts are relatively simplistic, and a number of cost calculations are approximate. The analysis provided here is based on the author's own understanding, and welcome any corrections or feedback.
[Infographic] Highlights | Database New Features in November 2024
Connection Skew after Tair (Redis® OSS-Compatible) Proxy RT Rise
ApsaraDB - October 24, 2023
ApsaraDB - August 7, 2023
ApsaraDB - May 24, 2024
Alibaba EMR - March 16, 2021
Alibaba EMR - May 20, 2022
Alibaba EMR - January 10, 2023
ApsaraDB RDS for MySQL
An on-demand database hosting service for MySQL with automated monitoring, backup and disaster recovery capabilities
Learn More
ApsaraDB RDS for PostgreSQL
An on-demand database hosting service for PostgreSQL with automated monitoring, backup and disaster recovery capabilities
Learn More
ApsaraDB RDS for MariaDB
ApsaraDB RDS for MariaDB supports multiple storage engines, including MySQL InnoDB to meet different user requirements.
Learn More
ApsaraDB RDS for SQL Server
An on-demand database hosting service for SQL Server with automated monitoring, backup and disaster recovery capabilities
Learn MoreMore Posts by ApsaraDB
