In a recent episode of the Super Brain (The Brain) show, a contestant from Google showed a system built when working for Google and displayed relationships among figures during the Three Kingdoms period. This is a typical graph application scenario.
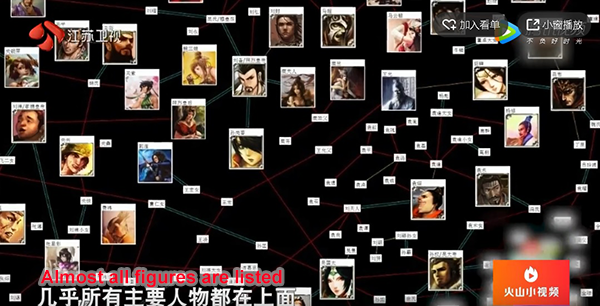
PostgreSQL is perfect for these scenarios due to its various SQL interfaces and excellent performance.
Similar to the preceding scenario, this document from one of the community member explains how to store family relationships and quickly extract N-tier information. This is similar to the article on social user relationships and risk control enterprise relationships that we wrote about before.
1. Create a personal information table that describes personal details such as year and month of birth, address, and city. Because not all personal information can be listed, JSON can be used to show information that is not mentioned. This is very useful.
create table tbl_p_detail -- Personal information
(
id int primary key, -- Family member ID
info jsonb, -- Family member description
crt_time timestamp -- Creation time
); 2. Create a relationship metadata table that stores relationships such as father, mother, husband, wife, son, daughter, adopted daughter, stepfather, godfather, and goddaughter.
create table tbl_er_desc -- Relationship description
(
id int2 primary key, -- Relationship ID
info text -- Description
); 3. Create a relationship table. In this example, we use two-way redundant storage to ensure the query accuracy (or simplify query statements). For example, store information about a father and a son as two entries.
create table tbl_er -- What is the family role of ID1 to ID2
(
c1 int references tbl_p_detail(id),
c2 int references tbl_p_detail(id),
prop int2[], -- Multiple relationships may exist. Therefore, we use array storage. This is an edge. Of course, we can also use JSON to store edges. For more information, refer to another article that I have written.
crt_time timestamp,
check (c1<>c2),
unique (c1,c2)
-- FOREIGN KEY (EACH ELEMENT OF prop) REFERENCES tbl_er_desc(id) -- Array foreign key, which is supported for PostgreSQL 11. The performance is good
); 4. Create indexes to implement acceleration
create index idx_tbl_er_c1 on tbl_er(c1);
create index idx_tbl_er_c2 on tbl_er(c2); 5. Write some data into the tables

insert into tbl_p_detail select generate_series(1,10000);
insert into tbl_er values (1,2,array[10],now()); -- For example, 1 is the father of 2
insert into tbl_er values (2,1,array[9],now()); -- For example, 2 is the daughter of 1
insert into tbl_er values (1,3,array[10],now()); -- For example, 1 is the father of 3
insert into tbl_er values (3,1,array[9],now()); -- For example, 3 is the daughter of 1
insert into tbl_er values (5,2,array[11],now()); -- For example, 5 is the mother of 2
insert into tbl_er values (2,5,array[9],now()); -- For example, 2 is the daughter of 5
insert into tbl_er values (5,3,array[11],now()); -- For example, 5 is the mother of 3
insert into tbl_er values (3,5,array[9],now()); -- For example, 3 is the daughter of 5
insert into tbl_er values (4,1,array[10],now()); -- For example, 4 is the father of 1
insert into tbl_er values (1,4,array[8],now()); -- For example, 1 is the son of 4
insert into tbl_er values (6,5,array[10],now()); -- For example, 6 is the father of 5
insert into tbl_er values (5,6,array[9],now()); -- For example, 5 is the daughter of 6
insert into tbl_er values (7,1,array[11],now()); -- For example, 7 is the mother of 1
insert into tbl_er values (1,7,array[8],now()); -- For example, 1 is the son of 7
insert into tbl_er values (8,5,array[11],now()); -- For example, 8 is the mother of 5
insert into tbl_er values (5,8,array[9],now()); -- For example, 5 is the daughter of 8 1. Search for a family member's N-tier relationship data and specify the limit on the records per tier. (Generally the volume of family data is not very large. Therefore we can simply limit the tier. It does not even matter if all results for each tier are returned.)
create or replace function graph_search1(
IN i_root int, -- The node that the search is based on
IN i_depth int default 99999, -- the tier to search (the depth limit)
IN i_limit int8 default 2000000000, -- limit the number of records returned for each tier
OUT o_path int[], -- output: path, an array of IDs
OUT o_point1 int, -- output: point 1 ID
OUT o_point2 int, -- output: point 2 ID
OUT o_link_prop int2[], -- output: the connection property between the two current points
OUT o_link_prop_all text, -- output: the connection property from the starting node to the current node
OUT o_depth int -- output: current depth (tier)
) returns setof record as
$$
declare
sql text;
begin
sql := format($_$
WITH RECURSIVE search_graph(
c1, -- point 1
c2, -- point 2
prop, -- current edge property
all_prop, -- properties of all edges
depth, -- current depth, starting from 1
path -- path, stored as an array
) AS (
select c1,c2,prop,all_prop,depth,path from (
SELECT -- ROOT node query
g.c1, -- point 1
g.c2, -- point 2
g.prop, -- edge property
g.prop::text as all_prop, -- properties of all edges
1 depth, -- initial depth=1
ARRAY[g.c1, g.c2] path -- initial path
FROM tbl_er AS g
WHERE
c1 = %s -- ROOT node=?
limit %s -- How many records are limited at each tier?
) t
UNION ALL
select c1,c2,prop,all_prop,depth,path from (
SELECT -- recursive clause
g.c1, -- point 1
g.c2, -- point 2
g.prop, -- edge property
sg.all_prop || g.prop::text as all_prop, -- properties of all edges
sg.depth + 1 depth, -- depth +1
sg.path || g.c2 path -- Add a new point to the path
FROM tbl_er AS g, search_graph AS sg -- circular INNER JOIN
WHERE
g.c1 = sg.c2 -- recursive JOIN condition
AND (g.c2 <> ALL(sg.path)) -- Prevent loop, determine whether it is a loop and judge if the new point is already in the previous path
AND sg.depth <= %s -- search depth =?
limit %s -- How many records are limited at each tier?
) t
)
SELECT path as o_path, c1 as o_point1, c2 as o_point2, prop as o_link_prop, all_prop as o_link_prop_all, depth as o_depth
FROM search_graph; -- query a recursive table. You can add LIMIT output or use a cursor
$_$, i_root, i_limit, i_depth, i_limit
);
return query execute sql;
end;
$$
language plpgsql strict; Example
postgres=# select * from graph_search1(1);
o_path | o_point1 | o_point2 | o_link_prop | o_link_prop_all | o_depth
-----------+----------+----------+-------------+-----------------+---------
{1,2} | 1 | 2 | {10} | {10} | 1
{1,3} | 1 | 3 | {10} | {10} | 1
{1,4} | 1 | 4 | {8} | {8} | 1
{1,7} | 1 | 7 | {8} | {8} | 1
{1,2,5} | 2 | 5 | {9} | {10}{9} | 2
{1,3,5} | 3 | 5 | {9} | {10}{9} | 2
{1,2,5,8} | 5 | 8 | {9} | {10}{9}{9} | 3
{1,2,5,6} | 5 | 6 | {9} | {10}{9}{9} | 3
{1,2,5,3} | 5 | 3 | {11} | {10}{9}{11} | 3
{1,3,5,8} | 5 | 8 | {9} | {10}{9}{9} | 3
{1,3,5,6} | 5 | 6 | {9} | {10}{9}{9} | 3
{1,3,5,2} | 5 | 2 | {11} | {10}{9}{11} | 3
(12 rows)
Time: 1.120 ms 2. Define a similar search function and return cursors. (Because number of relationships on a family pedigree is not very large, a cursor is not necessary. However, it is recommended to use cursors to return results for a social pedigree chart, which usually has a large volume of data.)
create or replace function graph_search2(
IN i_root int, -- The node that the search is based on
IN i_res name, -- cursor name
IN i_depth int default 99999, -- the tier to search (the depth limit)
IN i_limit int8 default 2000000000 -- Limit the number of records returned for each tier
) returns refcursor as
$$
declare
sql text;
res refcursor := i_res;
begin
sql := format($_$
WITH RECURSIVE search_graph(
c1, -- point 1
c2, -- point 2
prop, -- current edge property
all_prop, -- properties of all edges
depth, -- current depth, starting from 1
path -- path, stored using an array
) AS (
select c1,c2,prop,all_prop,depth,path from (
SELECT -- ROOT node query
g.c1, -- point 1
g.c2, -- point 2
g.prop, -- edge property
g.prop::text as all_prop, -- properties of all edges
1 depth, -- initial depth=1
ARRAY[g.c1, g.c2] path -- initial path
FROM tbl_er AS g
WHERE
c1 = %s -- ROOT node=?
limit %s -- How many records are limited at each tier?
) t
UNION ALL
select c1,c2,prop,all_prop,depth,path from (
SELECT -- recursive clause
g.c1, -- point 1
g.c2, -- point 2
g.prop, -- edge property
sg.all_prop || g.prop::text as all_prop, -- properties of all edges
sg.depth + 1 depth, -- depth + 1
sg.path || g.c2 path -- Add a new point to the path
FROM tbl_er AS g, search_graph AS sg -- circular INNER JOIN
WHERE
g.c1 = sg.c2 -- recursive JOIN condition
AND (g.c2 <> ALL(sg.path)) -- Prevent loop, determine whether it is a loop and judge if the new point is already in the previous path
AND sg.depth <= %s -- search depth =?
limit %s -- How many records are limited at each tier?
) t
)
SELECT path as o_path, c1 as o_point1, c2 as o_point2, prop as o_link_prop, all_prop as o_link_prop_all, depth as o_depth
FROM search_graph; -- query a recursive table. You can add LIMIT output or use a cursor
$_$, i_root, i_limit, i_depth, i_limit
);
open res for execute sql;
return res;
end;
$$
language plpgsql strict; Example
postgres=# begin;
BEGIN
Time: 0.096 ms
postgres=# select * from graph_search2(1,'a');
graph_search2
---------------
a
(1 row)
Time: 1.110 ms
postgres=# fetch 10 from a;
o_path | o_point1 | o_point2 | o_link_prop | o_link_prop_all | o_depth
-----------+----------+----------+-------------+-----------------+---------
{1,2} | 1 | 2 | {10} | {10} | 1
{1,3} | 1 | 3 | {10} | {10} | 1
{1,4} | 1 | 4 | {8} | {8} | 1
{1,7} | 1 | 7 | {8} | {8} | 1
{1,2,5} | 2 | 5 | {9} | {10}{9} | 2
{1,3,5} | 3 | 5 | {9} | {10}{9} | 2
{1,2,5,8} | 5 | 8 | {9} | {10}{9}{9} | 3
{1,2,5,6} | 5 | 6 | {9} | {10}{9}{9} | 3
{1,2,5,3} | 5 | 3 | {11} | {10}{9}{11} | 3
{1,3,5,8} | 5 | 8 | {9} | {10}{9}{9} | 3
(10 rows)
Time: 0.256 ms
postgres=# fetch 10 from a;
o_path | o_point1 | o_point2 | o_link_prop | o_link_prop_all | o_depth
-----------+----------+----------+-------------+-----------------+---------
{1,3,5,6} | 5 | 6 | {9} | {10}{9}{9} | 3
{1,3,5,2} | 5 | 2 | {11} | {10}{9}{11} | 3
(2 rows)
Time: 0.103 ms 3. Define the shortest path between two points. For example, search for the relationship between family members A and B When the relationship exceeds the N tier, no results are returned to avoid long-time searches. (We can also define a timeout statement to exit from the search when the execution exceeds N seconds.)
create or replace function graph_search3(
IN i_p1 int, -- point 1
IN i_p2 int, -- point 2
IN i_depth int default 99999, -- the tier to search (the depth limit)
OUT o_path int[], -- output: path, an array of IDs
OUT o_link_prop text, -- output: the connection property between the two current points
OUT o_depth int -- output: current depth (tier)
) returns record as
$$
declare
sql text;
begin
sql := format($_$
WITH RECURSIVE search_graph(
c1, -- point 1
c2, -- point 2
prop, -- edge property
depth, -- depth, starting from 1
path -- path, stored using an array
) AS (
SELECT -- ROOT node query
g.c1, -- point 1
g.c2, -- point 2
g.prop::text, -- edge property
1 depth, -- initial depth =1
ARRAY[g.c1, g.c2] path -- initial path
FROM tbl_er AS g
WHERE
c1 = %s -- ROOT node =? -- (the start of the shortest path)
UNION ALL
SELECT -- recursive clause
g.c1, -- point 1
g.c2, -- point 2
sg.prop::text || g.prop::text, -- edge property
sg.depth + 1 as depth, -- depth + 1
sg.path || g.c2 path -- Add a new point to the path
FROM tbl_er AS g, search_graph AS sg -- circular INNER JOIN
WHERE
g.c1 = sg.c2 -- recursive JOIN condition
AND (g.c2 <> ALL(sg.path)) -- Prevent loop, determine whether it is a loop and judge if the new point is already in the previous path
AND sg.depth <= %s -- search depth =?
)
SELECT
path as o_path,
prop as o_link_prop,
depth as o_depth
FROM search_graph
where c2 = %s -- the end of the shortest path
limit 1 -- query a recursive table. You can add LIMIT output or use a cursor
$_$, i_p1, i_depth, i_p2);
execute sql into o_path,o_link_prop,o_depth;
return;
end;
$$
language plpgsql strict; Example
postgres=# select * from graph_search3(1,2);
o_path | o_link_prop | o_depth
--------+-------------+---------
{1,2} | {10} | 1
(1 row)
Time: 0.907 ms
postgres=# select * from graph_search3(1,5);
o_path | o_link_prop | o_depth
---------+-------------+---------
{1,2,5} | {10}{9} | 2
(1 row)
Time: 0.854 ms
postgres=# select * from graph_search3(1,8);
o_path | o_link_prop | o_depth
-----------+-------------+---------
{1,2,5,8} | {10}{9}{9} | 3
(1 row) Add some relationships and search again
insert into tbl_er values (2,3,array[12],now()); -- For example, 2 is the elder sister of 3
insert into tbl_er values (3,2,array[13],now()); -- For example, 3 is the younger sister of 2
postgres=# select * from graph_search1(1);
o_path | o_point1 | o_point2 | o_link_prop | o_link_prop_all | o_depth
-------------+----------+----------+-------------+-----------------+---------
{1,2} | 1 | 2 | {10} | {10} | 1
{1,3} | 1 | 3 | {10} | {10} | 1
{1,4} | 1 | 4 | {8} | {8} | 1
{1,7} | 1 | 7 | {8} | {8} | 1
{1,2,3} | 2 | 3 | {12} | {10}{12} | 2
{1,2,5} | 2 | 5 | {9} | {10}{9} | 2
{1,3,2} | 3 | 2 | {13} | {10}{13} | 2
{1,3,5} | 3 | 5 | {9} | {10}{9} | 2
{1,2,3,5} | 3 | 5 | {9} | {10}{12}{9} | 3
{1,2,5,8} | 5 | 8 | {9} | {10}{9}{9} | 3
{1,2,5,6} | 5 | 6 | {9} | {10}{9}{9} | 3
{1,2,5,3} | 5 | 3 | {11} | {10}{9}{11} | 3
{1,3,2,5} | 2 | 5 | {9} | {10}{13}{9} | 3
{1,3,5,8} | 5 | 8 | {9} | {10}{9}{9} | 3
{1,3,5,6} | 5 | 6 | {9} | {10}{9}{9} | 3
{1,3,5,2} | 5 | 2 | {11} | {10}{9}{11} | 3
{1,2,3,5,8} | 5 | 8 | {9} | {10}{12}{9}{9} | 4
{1,2,3,5,6} | 5 | 6 | {9} | {10}{12}{9}{9} | 4
{1,3,2,5,8} | 5 | 8 | {9} | {10}{13}{9}{9} | 4
{1,3,2,5,6} | 5 | 6 | {9} | {10}{13}{9}{9} | 4
(20 rows)
postgres=# select * from graph_search1(3);
o_path | o_point1 | o_point2 | o_link_prop | o_link_prop_all | o_depth
-------------+----------+----------+-------------+-----------------+---------
{3,1} | 3 | 1 | {9} | {9} | 1
{3,5} | 3 | 5 | {9} | {9} | 1
{3,2} | 3 | 2 | {13} | {13} | 1
{3,1,7} | 1 | 7 | {8} | {9}{8} | 2
{3,1,4} | 1 | 4 | {8} | {9}{8} | 2
{3,1,2} | 1 | 2 | {10} | {9}{10} | 2
{3,5,8} | 5 | 8 | {9} | {9}{9} | 2
{3,5,6} | 5 | 6 | {9} | {9}{9} | 2
{3,5,2} | 5 | 2 | {11} | {9}{11} | 2
{3,2,5} | 2 | 5 | {9} | {13}{9} | 2
{3,2,1} | 2 | 1 | {9} | {13}{9} | 2
{3,1,2,5} | 2 | 5 | {9} | {9}{10}{9} | 3
{3,5,2,1} | 2 | 1 | {9} | {9}{11}{9} | 3
{3,2,5,8} | 5 | 8 | {9} | {13}{9}{9} | 3
{3,2,5,6} | 5 | 6 | {9} | {13}{9}{9} | 3
{3,2,1,7} | 1 | 7 | {8} | {13}{9}{8} | 3
{3,2,1,4} | 1 | 4 | {8} | {13}{9}{8} | 3
{3,1,2,5,8} | 5 | 8 | {9} | {9}{10}{9}{9} | 4
{3,1,2,5,6} | 5 | 6 | {9} | {9}{10}{9}{9} | 4
{3,5,2,1,7} | 1 | 7 | {8} | {9}{11}{9}{8} | 4
{3,5,2,1,4} | 1 | 4 | {8} | {9}{11}{9}{8} | 4
(21 rows) Facebook LinkBench Tests PostgreSQL Social Relation Profile Scenario Performance
PostgreSQL Feed Systems Similar to Weibo - Design and Performance Metrics
digoal - July 4, 2019
digoal - July 4, 2019
digoal - July 4, 2019
Alibaba Cloud Community - June 28, 2023
ApsaraDB - February 24, 2026
Alibaba Clouder - November 26, 2019
 ApsaraDB RDS for PostgreSQL
ApsaraDB RDS for PostgreSQL
An on-demand database hosting service for PostgreSQL with automated monitoring, backup and disaster recovery capabilities
Learn More PolarDB for PostgreSQL
PolarDB for PostgreSQL
Alibaba Cloud PolarDB for PostgreSQL is an in-house relational database service 100% compatible with PostgreSQL and highly compatible with the Oracle syntax.
Learn More ApsaraDB RDS for MySQL
ApsaraDB RDS for MySQL
An on-demand database hosting service for MySQL with automated monitoring, backup and disaster recovery capabilities
Learn More ApsaraDB for OceanBase
ApsaraDB for OceanBase
A financial-grade distributed relational database that features high stability, high scalability, and high performance.
Learn MoreMore Posts by digoal