This topic introduces the basic concepts of Trajectory SQL.
Trajectory objects
Concept | Description |
Trajectory Point | The spatio-temporal object that consists of the spatial location and attributes of a moving object at a specific point in time. The spatial location can be represented by 2D or 3D coordinates. The attributes can be a number of fields that use different data types. |
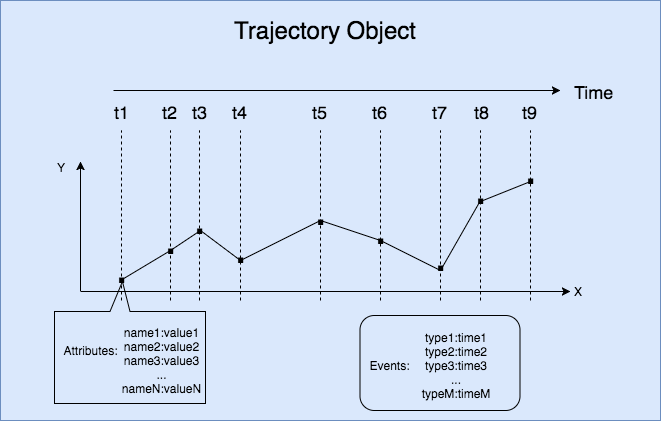
Trajectory Object | The high-dimensional object that consists of trajectory points and events. Specifically, the high-dimensional object includes time, space, attributes, and events. |
Trajectory Timeline | The time value sequence of a trajectory. The time values in the sequence must be consecutive. |
Trajectory Spatial | The spatial geometry of a trajectory. In most cases, the spatial geometry is described by using the LineString data type. |
Trajectory Leaf | The spatial location of a moving object at a specific point in time. The spatial location is a trajectory point. |
Trajectory Attributes | The attributes that describe the trajectory of a moving object at different trajectory points. These attributes include velocity and direction. |
Trajectory Attribute Field | The attribute field that describes the trajectory of a moving object. The number of values for an attribute field, such as the velocity field, is the same as the number of trajectory points of the moving object. |
Trajectory Field Value | The value of an attribute field at a specific point in time. |
Trajectory Events | The events that occur along a trajectory. For example, these events include the refueling, breakdown, and car lock events of a moving car along the trajectory. An event consists of the event type ID and the event time. |
The following figure shows the trajectory of a moving object.
BoxNDF objects
Computing on trajectory-related objects, including trajectories and geometries, is complex. Cubes are easier to calculate than these trajectory-related objects and may be used to describe queries or simplify computing operations. The BoxNDF data type is used to describe cubes.
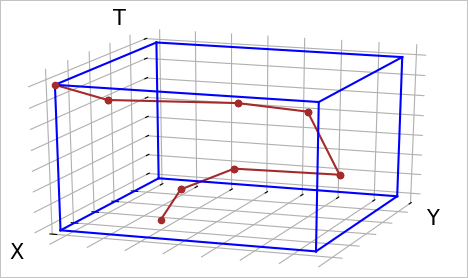
A BoxNDF object is a multi-dimensional spatio-temporal cube that is expressed by the minimum and maximum values on the following four coordinate axes: x, y, z, and t. The z-axis represents space, and the t-axis represents time. Cubes can include different axes. For example, cubes can include the x-axis and y-axis or include the x-axis, y-axis, z-axis, and t-axis.
When you run a query, you can use a cube to specify the query scope. In addition, you can use the bounding box of a trajectory or a geometry to facilitate the query. The following figure shows the trajectory and bounding box of an object that moves on the x-axis, y-axis, and t-axis.
The following figure shows the bounding box of an object.
Data types for time values in PostgreSQL
PostgreSQL supports the following data types for time values:
TIMESTAMPTZ: a time value with information about the time zone.
TIMESTAMP: a time value without information about the time zone.
INTERVAL: a time range.
In the trajectory module of GanosBase, the TIMESTAMP type is used and the INTERVAL type is used to facilitate computing. In most cases, a TIMESTAMP value is expressed as a string, such as 2000-01-01 10:00:00. The following statements show common operations on time values:
-- Create a time value of the TIMESTAMP type.
SELECT '2000-01-01 10:00:00'::timestamp;
-- Convert a UNIX timestamp to a time value of the TIMESTAMP type. The ganos_trajectory extension is required.
SELECT ST_UnixEpochToTS(1649765331);
-- Convert a time value of the TIMESTAMP type to a UNIX timestamp.
SELECT ST_TsToUnixEpoch('2022-04-12 12:08:51');
-- Add a value of the INTERVAL type to a time value or subtract a value of the INTERVAL type from a time value.
SELECT '2000-01-01 10:00:00'::timestamp + '30 day'::interval;
SELECT '2000-01-01 10:00:00'::timestamp - '1 month'::interval;Geometries in GanosBase
A geometry in GanosBase is an object that can be a point, line, or polygon in two dimensions or three dimensions. GanosBase is compatible with PostGIS interfaces. In the trajectory module of GanosBase, multiple spatial computations between trajectories and geometries are supported.
-- Construct a point (2,4).
SELECT 'POINT(2 4)'::geometry;
-- Construct a broken line (2,4)->(0,0)->(5,3).
SELECT 'LINESTRING(2 4, 0 0, 5 3)';
-- Construct a polygon. In this example, a triangle whose vertices are (3,3), (2,2), and (5,5) is constructed.
SELECT 'POLYGON(3 3, 5 5, 2 2, 3 3)';
-- Construct a circle with (0,1) as the center and a radius of 3. The circle is approximated by a polygon. In most cases, functions such as ST_DistanceWithin rather than ST_Buffer are used to query the intersections of circles.
SELECT ST_Buffer('POINT(0 1)', 3);In 2D space, the preceding statements can be directly used. Euclidean distances are not suitable in some scenarios. If you calculate the distance between two points that are expressed by using latitude and longitude, you must calculate the distance between the points on the surface of the Earth, not the Euclidean distance. In some cases, you are required to measure the distance in meters. The spatial reference identifier (SRID) is set to 4326 for latitudes and longitudes. SRID 4326 indicates that the World Geodetic System 1984 (WGS84) system is used.
-- Construct a point (2,4).
SELECT 'SRID=4326;POINT(2 4)'::geometry;
-- Construct a broken line (2,4)->(0,0)->(5,3).
SELECT 'SRID=4326;LINESTRING(2 4, 0 0, 5 3)';
-- Construct a polygon. In this example, a triangle whose vertices are (3,3), (2,2), and (5,5) is constructed.
SELECT 'SRID=4326;POLYGON(3 3, 5 5, 2 2, 3 3)';
-- Construct a circle with (0,1) as the center and a radius of 3. The circle is approximated by a polygon. In most cases, functions such as ST_DistanceWithin rather than ST_Buffer are used to query the intersections of circles.
SELECT ST_SetSRID(ST_Buffer('POINT(0 1)', 3),4326);The coordinates of points vary based on the projected coordinate system (PCS). To facilitate distance calculations, you can convert the latitude and longitude coordinates into coordinates in meters.
-- Convert the PCS to EPSG:3857, which is a Spherical Mercator projected coordinate system popularized by web services such as Google services. In this system, meters are used to measure points. EPSG:3857 is commonly used in map applications.
SELECT ST_Transform('SRID=4326;POINT(114 39)'::geometry, 3857);
-- Convert the PCS to EPSG:4479, a more accurate Gauss Kruger projection for China.
SELECT ST_Transform('SRID=4326;POINT(114 39)'::geometry, 4479);