Background information
The recommendation system selects the items that are shown to users and expects positive user behavior such as click and buy. However, the recommendation system cannot predict user behavior when the system recommends an item to a user, which indicates that the system cannot learn the rewards of the recommendation in advance. The recommendation system must keep trying and collect user behavioral data in real time to update the recommendation policies. This minimizes the regret. The process is similar to a gambler playing slot machines. In a gambling house, a gambler stands in front of a row of slot machines. Each machine provides a random reward from a probability distribution specific to that machine. The gambler has to decide which machines to play and in which order to play them so as to maximize the sum of rewards. This is the multi-armed bandit (MAB) problem.
The MAB problem exemplifies the exploration–exploitation tradeoff dilemma. Exploitation indicates that the gambler needs to play the machines that are known to have high payoffs to obtain more rewards. Exploration indicates that the gambler also needs to play other machines so as not to miss better payoffs. However, in this case, the gambler also faces higher risks, and opportunity costs are increased.
Cold start problem
New items do not have historical behavioral data. How do I allocate traffic to maximize user satisfaction?
Feedback loops in a recommendation system
The recommendation algorithms determine the content to be displayed, the displayed content affects user behavior, and user behavioral data is collected to train the algorithm models. In this case, feedback loops occur. In feedback loops, data in the training dataset and test dataset are not independently or identically distributed. In addition, the system does not have an effective exploration mechanism. The algorithm models focus more on local optimization.
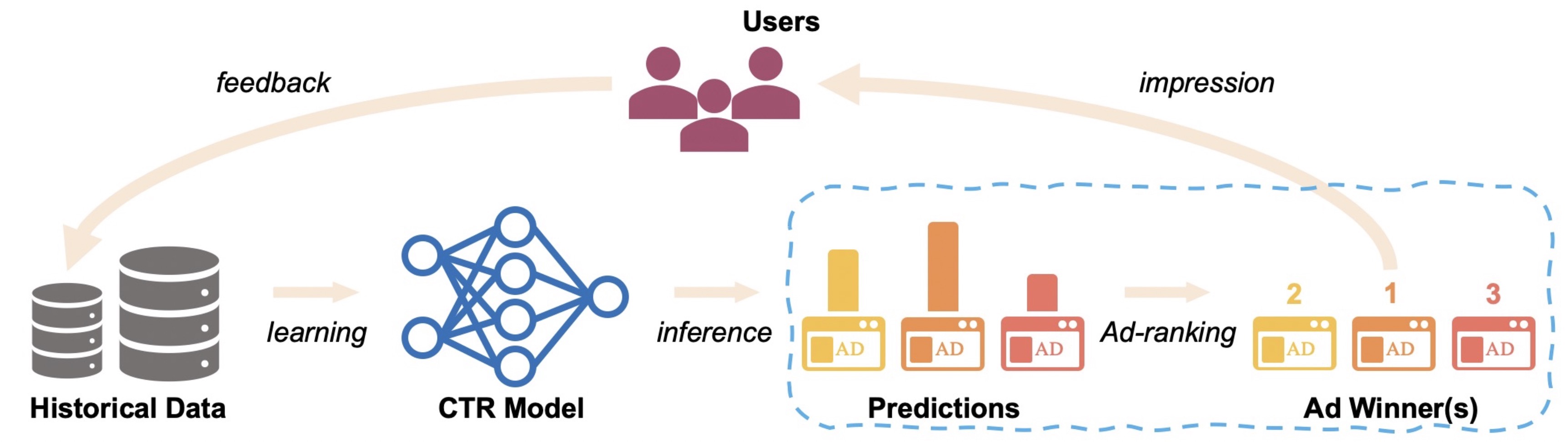
If user behavioral data is sparse, negative feedback loops are more serious. The key issue is that limited data cannot be used to predict recommendation performance with absolute confidence. Exploration and exploitation are essential to close negative feedback loops.
Overview
Bandit algorithms can better balance exploration and exploitation. You do not need to collect a large amount of data in advance to resolve the cold start problem. This prevents the Matthew effect from being generated by weight calculation based on direct benefits divided by the number of exposures. In addition, the recommendation system can have a chance to expose most long-tail items and new items. The recommendation algorithms designed based on bandit algorithms can better resolve the preceding issues.
Bandit algorithms are classified into context-free and contextual bandit algorithms based on whether context characteristics are considered.
Pseudocode of single-play bandit algorithms:
Differences between bandit algorithms and traditional algorithms:
Each candidate item corresponds to an independent model. This avoids the unbalanced sample distribution in traditional models in which all items correspond to one model.
The traditional algorithms adopt greedy policies and focus on exploitation to utilize existing knowledge as much as possible. This may cause information cocoons due to the Matthew effect. However, bandit algorithms are featured with explicit exploration mechanisms. The items with less exposure obtain more exposure chances.
Bandit algorithms are based on online learning and update their models in real time. Bandit algorithms can obtain the optimal policy faster than A/B testing.
To recommend multiple candidate items in a request, use the following multiple-play bandit algorithm.

Detailed description
Bandit algorithms are policies used to solve the exploitation-exploration dilemma. Bandit algorithms are classified into context-free and contextual bandit algorithms based on whether context features are considered.
1. UCB
Context-free bandit algorithms include the epsilon-greedy, softmax, Thompson sampling, and upper confidence bound (UCB).
The UCB refers to the upper limit of the confidence interval for the mean reward and indicates the estimated value of the future reward for a specific arm.
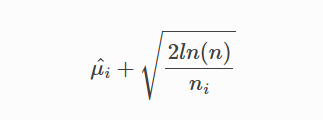
The arm with the highest UCB is chosen. The advantage of the UCB algorithm is to provide more chances for unknown arms.
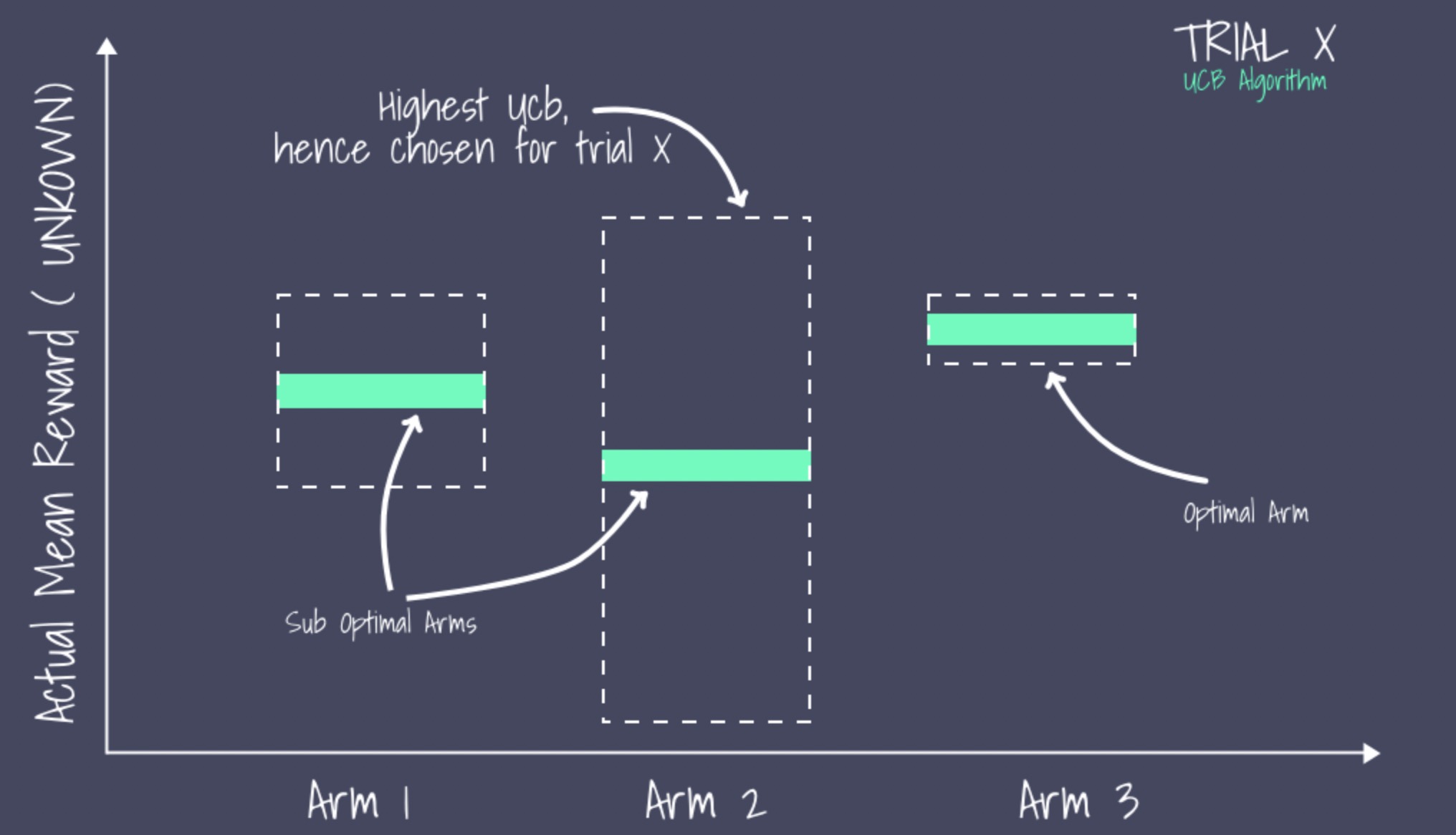
The mean reward of unknown and less pulled arms may be low. However, the UCB of these arms may be high due to uncertainties. Therefore, the exploration mechanism can be triggered with a high probability.
The exploitation mechanism is more likely to be triggered for known arms. If the mean reward of an arm is great, more chances are given to pull the arm. Otherwise, fewer chances are given.
2. LinUCB
In a recommendation system, items that are to be recommended are usually regarded as the arms of the MAB problem. Context-free bandit algorithms such as the UCB algorithm do not take into account the context information in a recommendation scene and use the same policy to recommend items to all users. This way, user features, such as their interest, preference, and purchasing power, are neglected. The same item is accepted differently by different users in different scenes. Therefore, recommendation systems do not employ context-free bandit algorithms.
Contextual bandit algorithms take into account the context information when they are used to solve the exploitation-exploration dilemma. Therefore, contextual bandit algorithms are applicable to personalized recommendation scenes.
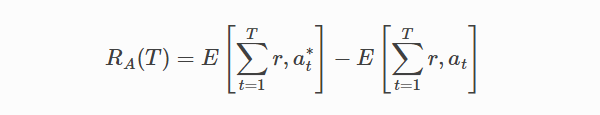
T indicates all "t" in a trial. at* is the arm with the maximum expected payoff at trial t, which you cannot know in advance.
Advantages of the LinUCB algorithm:
The computational complexity is linear with the number of arms.
The dynamic candidate arms are supported.
References
Implement contextual bandit algorithms in recommendation systems
Experience and traps of deploying contextual bandit (LinUCB) algorithms in recommendation systems in production environments
Using Multi-armed Bandit to Solve Cold-start Problems in Recommender Systems at Telco
A Multiple-Play Bandit Algorithm Applied to Recommender Systems
Adapting multi-armed bandits polices to contextual bandits scenarios