Rapidly increasing volume of published content poses content optimization challenges for online sites. For instance, a trending event may be reported via many media, a good article may be reproduced by various readers, or a product/group of products may be pushed or promoted by many advertisement platforms or shopping guide platforms. This leads to a scenario where shopping guide websites, news media, technical forums, and search engines may have many similar or even duplicate articles or images.
These are minor issues if interests are not involved. However, problems may escalate if the vested interests of the parties involved are at stake.
For example, in an e-commerce scenario, shopping guide websites receive recommendation articles from various social groups. Such recommendation articles introduce many products and provide information about using these products. If an article covers most products in a manner similar to an already published shopping guide article, then usually such an article is not published to avoid a clash of interests.
Therefore, it is critical for websites to avoid publishing any similar or duplicate content. Usually, websites employ a machine review mechanism or assign personnel to review recommendation content to prevent similar or duplicate articles. However, manual review suffers serious bottlenecks, while machine review faces asynchronous batch review issues as every new article needs to be compared against all historical articles. So, the important question that arises is whether there are any technologies that support real-time content review by comparing each new article with all the existing ones?
The answer would be Yes, PostgreSQL technologies are ideal to address such challenges. This article gives you a walkthrough on how PostgreSQL technologies help to optimize e-Commerce content.
This section describes a content deduplication case to help you understand the concept better. On a shopping guide platform, every article recommends several products and give their basic introduction. For example, you may be visiting a shopping guide platform and be viewing an article that recommends toys.
Similarly, based on historical recommendations, there may be tens of millions to hundreds of millions of shopping guide articles. Further, each article may recommend dozens of products. Therefore, there may be tens of millions of recommended products. Also, hot products, such as bestsellers, are normally recommended in many articles. Moreover, some sellers may also pay fees to improve the frequency of recommendations generated for their products.
Let's consider the following example to understand how to use the PostgreSQL smlar plug-in to deduplicate shopping guide articles in a timely manner. For more information about the smlar plug-in, you can check this document.
Now, assume that 1/5 of products in the shopping guide article library are hot products. Create a test database with 60 million shopping guide articles that involve 10 million products. Each article introduces 11 to 50 products. Products with IDs set to 1 to 500,000 are hot products, which are recommended by 10 million articles.
Step 1. Create the smlar plug-in.
create extension smlar;
Step 2. Create a test table.
create unlogged table test (
id serial, -- 文章ID
arr int8[] -- 商品ID组成的数组,假设商品ID为int8类型,那么数组就是int8[]
);
Step 3. Insert 50 million records to the table. The requirements for this are as follows:
The int8 value range is from 1 to 10 million. Considering that there are 10 million recommended products.
The length of the int8[ ] array is from 11 to 50. As each article contains 11 to 50 products
The records are evenly distributed.
The following commands show the test data insertion function. Each time the function is called, 40 records are inserted.
create or replace function f() returns void as $$
declare
begin
for i in 11..50 loop
insert into test (arr) select array_agg((10000000*random())::int8) from generate_series(1,i);
end loop;
end;
$$ language plpgsql strict;
Use pgbench to call the preceding function. 50 million test data records will be generated.
vi test.sql
select f();
pgbench -M prepared -n -r -P 1 -f ./test.sql -c 100 -j 100 -t 12500
Step 4. Generate the recommendation data of 10 million hot products. For example, products with IDs set to 1 to 500,000 are hot products, which are recommended by 10 million articles.
Modify the preceding function.
create or replace function f() returns void as $$
declare
begin
for i in 11..50 loop
insert into test (arr) select array_agg((500000*random())::int8) from generate_series(1,i);
end loop;
end;
$$ language plpgsql strict;
Use pgbench to call the preceding function to generate 10 million test data records.
pgbench -M prepared -n -r -P 1 -f ./test.sql -c 100 -j 100 -t 2500
Data for 60 million recommendation articles are generated.
Step 5. Now, create a GIN index and use the OPS provided by the smlar plug-in.
set maintenance_work_mem='64GB';
create index on test using gin ( arr _int8_sml_ops );
虽然smlar插件还支持 gist 索引,但是本文的CASE不建议使用gist索引
-- create index on test using gist ( arr _int8_sml_ops );
Step 6. Next, implement the similarity calculation algorithms. The smlar plug-in supports several default algorithms and custom formulas. Note that the following parameters indicate the results after array element deduplication.
N. i: number of intersected elements
N. a: number of elements in the first array
N. b: number of elements in the second array
The default algorithms are as follows:
Step 6.1. Cosine: N.i/sqrt (N.a x N.b)
Step 6.2. Overlap: N.i
Step 6.3. TF-IDF: It is complex. For more information, refer to my blog post (in Chinese): Application of PostgreSQL Together with Cosine and Linear Correlation Algorithms in the Text, Image, and Array Similarity Fields (2) - smlar Plug-in Introduction
The configuration method is shown as below.
允许普通用户设置,会话级别,会话之间互不干扰。
set smlar.type='cosine';
-- set smlar.type='overlap';
-- set smlar.type='tfidf';
Refer to the following custom formulas to understand their usage.
float4 smlar( anyarray a, anyarray b, text formula );
- computes similary of two arrays by given formula, arrays should
be the same type.
Predefined variables in formula:
N.i - number of common elements in both array (intersection)
N.a - number of uniqueelements in first array
N.b - number of uniqueelements in second array
Example:
smlar('{1,4,6}'::int[], '{5,4,6}' )
smlar('{1,4,6}'::int[], '{5,4,6}', 'N.i / sqrt(N.a * N.b)' ) -- 第三个参数为自定义公式
That calls are equivalent.
Step 7. Next, you need to test performance. If an article on a shopping guide website recommends 10 products and 9 of those are the same as mentioned in another shopping guide article, this article is regarded as a duplicate article and will be rejected. You can also set the threshold for the number of the same products in different articles based on your own requirements.
If 10 recommended products in a shopping guide article occurs in another 10 articles with one product in each article, the article will be approved.
The preceding example uses the overlap formula to determine the similarity.
You can retrieve some existing records and create test data to determine the similarity.
select arr from test limit 100;
Step 7.1 Use functions to simplify SQL statements.
create or replace function ff(
v_type text, -- 使用什么公式, tfidf or overlap or cosine
v_threshold float8, -- 设置对应公式的阈值
v_arr int8[] -- 要比较的数组
) returns boolean as $$
declare
begin
set enable_seqscan = off; -- 关闭全表扫描, 强制使用索引
execute format('set smlar.type=%L', v_type); -- 设置公式, overlap
-- threshold允许普通用户设置,会话之间互不干扰
execute format('set smlar.threshold=%s', v_threshold); -- 设置相交元素个数的阈值, 这个阈值可以程序计算,也可以程序提供一个百分比,在PG中计算。建议程序自己算,减少数据库开销。
perform 1 from test where arr % v_arr limit 1; -- 搜索test表中arr字段与传入的v_arr值,判断是否有相似记录
if found then
set enable_seqscan = on; -- 退出函数时,恢复设置
return false; -- found similar array,表示找到了相似文章
else
set enable_seqscan = on; -- 退出函数时,恢复设置
return true; -- 表示没有找到相似文章
end if;
end;
$$ language plpgsql strict;
Step 7.2 Test scenario: forty common products.
High similarity with 4 ms response time
set enable_seqscan=off;
set smlar.type='overlap';
set smlar.threshold=39;
select id,arr,smlar(arr,'{9824126,8385751,3431657,4702366,536881,4432069,4646244,8071695,9493653,576176,343683,920351,505115,492412,3517002,8301249,1851489,3729325,5420033,9366936,9553716,4903162,2840830,965295,1125073,3061027,1831144,9210503,5385795,8519636,5369934,5209921,6905387,8801592,9912287,7442268,3233661,4558531,5513963,2727314,5134707,5857647,3647665,5639822,6350059,7164667,3941070,8201548,893992,9361104}'::int8[], 'N.i') as overlap
from test
where arr % '{9824126,8385751,3431657,4702366,536881,4432069,4646244,8071695,9493653,576176,343683,920351,505115,492412,3517002,8301249,1851489,3729325,5420033,9366936,9553716,4903162,2840830,965295,1125073,3061027,1831144,9210503,5385795,8519636,5369934,5209921,6905387,8801592,9912287,7442268,3233661,4558531,5513963,2727314,5134707,5857647,3647665,5639822,6350059,7164667,3941070,8201548,893992,9361104}'::int8[] limit 1;
postgres=# explain (analyze,verbose,timing,costs,buffers) select id,arr,smlar(arr,'{9824126,8385751,3431657,4702366,536881,4432069,4646244,8071695,9493653,576176,343683,920351,505115,492412,3517002,8301249,1851489,3729325,5420033,9366936,9553716,4903162,2840830,965295,1125073,3061027,1831144,9210503,5385795,8519636,5369934,5209921,6905387,8801592,9912287,7442268,3233661,4558531,5513963,2727314,5134707,5857647,3647665,5639822,6350059,7164667,3941070,8201548,893992,9361104}'::int8[], 'N.i') as overlap
from test where arr % '{9824126,8385751,3431657,4702366,536881,4432069,4646244,8071695,9493653,576176,343683,920351,505115,492412,3517002,8301249,1851489,3729325,5420033,9366936,9553716,4903162,2840830,965295,1125073,3061027,1831144,9210503,5385795,8519636,5369934,5209921,6905387,8801592,9912287,7442268,3233661,4558531,5513963,2727314,5134707,5857647,3647665,5639822,6350059,7164667,3941070,8201548,893992,9361104}'::int8[] limit 1;
QUERY PLAN
-------------------------------------------------------------------------------
Limit (cost=1013.60..1014.85 rows=1 width=274) (actual time=4.875..4.876 rows=1 loops=1)
Output: id, arr, (smlar(arr, '{9824126,8385751,3431657,4702366,536881,4432069,4646244,8071695,9493653,576176,343683,920351,505115,492412,3517002,8301249,1851489,3729325,5420033,9366936,9553716,4903162,2840830,965295,1125073,3061027,18
31144,9210503,5385795,8519636,5369934,5209921,6905387,8801592,9912287,7442268,3233661,4558531,5513963,2727314,5134707,5857647,3647665,5639822,6350059,7164667,3941070,8201548,893992,9361104}'::bigint[], 'N.i'::text))
Buffers: shared hit=202
-> Bitmap Heap Scan on public.test (cost=1013.60..76009.06 rows=60000 width=274) (actual time=4.874..4.874 rows=1 loops=1)
Output: id, arr, smlar(arr, '{9824126,8385751,3431657,4702366,536881,4432069,4646244,8071695,9493653,576176,343683,920351,505115,492412,3517002,8301249,1851489,3729325,5420033,9366936,9553716,4903162,2840830,965295,1125073,30610
27,1831144,9210503,5385795,8519636,5369934,5209921,6905387,8801592,9912287,7442268,3233661,4558531,5513963,2727314,5134707,5857647,3647665,5639822,6350059,7164667,3941070,8201548,893992,9361104}'::bigint[], 'N.i'::text)
Recheck Cond: (test.arr % '{9824126,8385751,3431657,4702366,536881,4432069,4646244,8071695,9493653,576176,343683,920351,505115,492412,3517002,8301249,1851489,3729325,5420033,9366936,9553716,4903162,2840830,965295,1125073,3061027
,1831144,9210503,5385795,8519636,5369934,5209921,6905387,8801592,9912287,7442268,3233661,4558531,5513963,2727314,5134707,5857647,3647665,5639822,6350059,7164667,3941070,8201548,893992,9361104}'::bigint[])
Heap Blocks: exact=1
Buffers: shared hit=202
-> Bitmap Index Scan on test_arr_idx (cost=0.00..998.60 rows=60000 width=0) (actual time=4.810..4.810 rows=1 loops=1)
Index Cond: (test.arr % '{9824126,8385751,3431657,4702366,536881,4432069,4646244,8071695,9493653,576176,343683,920351,505115,492412,3517002,8301249,1851489,3729325,5420033,9366936,9553716,4903162,2840830,965295,1125073,306
1027,1831144,9210503,5385795,8519636,5369934,5209921,6905387,8801592,9912287,7442268,3233661,4558531,5513963,2727314,5134707,5857647,3647665,5639822,6350059,7164667,3941070,8201548,893992,9361104}'::bigint[])
Buffers: shared hit=201
Planning time: 0.099 ms
Execution time: 4.910 ms
(13 rows)
Low similarity with 4 ms response time
set smlar.threshold=20;
select id,arr,smlar(arr,'{}'::int8[],'N.i') as overlap
from test
where arr % '{}'::int8[] limit 1;
Non-exist with 4 ms response time
set smlar.threshold=40;
select id,arr,smlar(arr,'{}'::int8[],'N.i') as overlap
from test
where arr % '{}'::int8[] limit 1;
Step 7.3 Test Scenario: ten hot products and thirty common products.
8790997,6822070,9034458,7045729,7426339,4870927,9298344,9841045,9653498,5049021,592665,9202806,6141445,534620,5208898,2370105,9546145,7383597,5658020,3118646,4081961,8268545,4748855,3798658,1595104,5408571,5865833,5432299,5893431,1814110,477735,220233,401904,426917,64745,266448,156966,27816,258082,138729
High similarity with 6 ms response time
set smlar.threshold=39;
select id,arr,smlar(arr,'{8790997,6822070,9034458,7045729,7426339,4870927,9298344,9841045,9653498,5049021,592665,9202806,6141445,534620,5208898,2370105,9546145,7383597,5658020,3118646,4081961,8268545,4748855,3798658,1595104,5408571,5865833,5432299,5893431,1814110,477735,220233,401904,426917,64745,266448,156966,27816,258082,138729}'::int8[],'N.i') as overlap
from test
where arr % '{8790997,6822070,9034458,7045729,7426339,4870927,9298344,9841045,9653498,5049021,592665,9202806,6141445,534620,5208898,2370105,9546145,7383597,5658020,3118646,4081961,8268545,4748855,3798658,1595104,5408571,5865833,5432299,5893431,1814110,477735,220233,401904,426917,64745,266448,156966,27816,258082,138729}'::int8[] limit 1;
Low similarity with 6 ms response time
set smlar.threshold=20;
Non-exist with 6 ms response time
set smlar.threshold=40;
Step 7.4. Test scenario: forty hot products.
267238,262959,96771,64156,264782,344608,162583,240894,206902,434057,378718,395427,342928,102342,69040,400565,360688,351453,160160,144552,420616,137895,364785,322520,64812,429531,88969,221778,457346,347051,360506,224584,110011,457277,288740,374792,301885,451323,115687,8788
High similarity with 15 ms response time
set smlar.threshold=39;
select id,arr,smlar(arr,'{267238,262959,96771,64156,264782,344608,162583,240894,206902,434057,378718,395427,342928,102342,69040,400565,360688,351453,160160,144552,420616,137895,364785,322520,64812,429531,88969,221778,457346,347051,360506,224584,110011,457277,288740,374792,301885,451323,115687,8788}'::int8[],'N.i') as overlap
from test
where arr % '{267238,262959,96771,64156,264782,344608,162583,240894,206902,434057,378718,395427,342928,102342,69040,400565,360688,351453,160160,144552,420616,137895,364785,322520,64812,429531,88969,221778,457346,347051,360506,224584,110011,457277,288740,374792,301885,451323,115687,8788}'::int8[] limit 1;
Low similarity with 15 ms response time
set smlar.threshold=20;
Non-exist with 15 ms response time
set smlar.threshold=40;
Step 7.5 Conduct a stress test where there are 35 common products, 5 hot products, and the overlap value is 35.
create or replace function bench() returns boolean as $$
declare
v_arr int8[];
begin
-- 生成40个商品的数组,其中普通商品35个,热点商品5个
select array_agg(id) into v_arr from (select (500000+random()*9500000)::int8 id from generate_series(1,35) union all select (random()*500000)::int8 id from generate_series(1,5) ) t;
-- 调用ff, 并返回结果, overlap=35,即满足35个相似的为相似文本
return ff('overlap', 35, v_arr);
end;
$$ language plpgsql strict;
Use pgbench to conduct a stress test.
vi test.sql
select bench();
pgbench -M prepared -n -r -P 1 -f ./test.sql -c 64 -j 64 -T 100
The stress test result shows that TPS is about 9,400, and CPU resources are used up.
progress: 97.0 s, 9513.0 tps, lat 6.726 ms stddev 1.495
progress: 98.0 s, 9556.0 tps, lat 6.695 ms stddev 1.441
progress: 99.0 s, 9501.0 tps, lat 6.731 ms stddev 1.524
progress: 100.0 s, 9659.3 tps, lat 6.626 ms stddev 1.203
transaction type: ./test.sql
scaling factor: 1
query mode: prepared
number of clients: 64
number of threads: 64
duration: 100 s
number of transactions actually processed: 945643
latency average = 6.762 ms
latency stddev = 1.515 ms
tps = 9455.190803 (including connections establishing)
tps = 9460.748975 (excluding connections establishing)
script statistics:
- statement latencies in milliseconds:
6.766 select bench();
Step 8. You can also use various other test queries, such as.
set smlar.type='overlap';
set smlar.threshold=2;
explain (analyze,verbose,timing,costs,buffers)
select
*,
smlar( arr, '{1,2,3,4,5}'::int8[], 'N.i' )
from
test
where
arr % '{1,2,3,4,5}'::int8[] -- where cosine similarity >= smlar.threshold
order by
smlar( arr, '{1,2,3,4,5}'::int8[] , 'N.i' ) desc
limit 10;
QUERY PLAN
---------------------------------------------------------------------------------------------------------------------------------------
Limit (cost=76837.64..76837.66 rows=10 width=274) (actual time=0.523..0.523 rows=0 loops=1)
Output: id, arr, (smlar(arr, '{1,2,3,4,5}'::bigint[], 'N.i'::text))
Buffers: shared hit=21
-> Sort (cost=76837.64..76987.64 rows=60000 width=274) (actual time=0.521..0.521 rows=0 loops=1)
Output: id, arr, (smlar(arr, '{1,2,3,4,5}'::bigint[], 'N.i'::text))
Sort Key: (smlar(test.arr, '{1,2,3,4,5}'::bigint[], 'N.i'::text)) DESC
Sort Method: quicksort Memory: 25kB
Buffers: shared hit=21
-> Bitmap Heap Scan on public.test (cost=545.60..75541.06 rows=60000 width=274) (actual time=0.514..0.514 rows=0 loops=1)
Output: id, arr, smlar(arr, '{1,2,3,4,5}'::bigint[], 'N.i'::text)
Recheck Cond: (test.arr % '{1,2,3,4,5}'::bigint[])
Buffers: shared hit=21
-> Bitmap Index Scan on test_arr_idx (cost=0.00..530.60 rows=60000 width=0) (actual time=0.509..0.509 rows=0 loops=1)
Index Cond: (test.arr % '{1,2,3,4,5}'::bigint[])
Buffers: shared hit=21
Planning time: 0.100 ms
Execution time: 0.566 ms
set smlar.threshold=1;
postgres=# select
*,
smlar( arr, '{1,2,3,4,5}'::int8[], 'N.i' )
from
test
where
arr % '{1,2,3,4,5}'::int8[] -- where cosine similarity >= smlar.threshold
order by
smlar( arr, '{1,2,3,4,5}'::int8[] , 'N.i' ) desc
limit 10;
id | arr
| smlar
---------+-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------------------------------------------------------------+-------
247838 | {237675,4661601,7866637,1488686,6727125,4429671,1737244,1298649,5000070,3005575,5226803,3932647,2649001,8069658,6161176,8361766,2525409,8765570,326152,2701673,3359631,2,1779920,2302730,1790402,4052782,5309527,9050565,5105087,5
147167,7750613,5342762,9808768,5617250,6831448,6535893,46921,8568692,7834542,5046991,1574267,3061345,8979638,4223268,1131003,5140814,2585034,3656412} | 1
599383 | {2236159,1910889,8347171,9808321,984302,9879937,8323590,8329741,3659904,5927698,3313023,3700527,5,1379483,624821,2545660,1107329,1008684,5866894,6913711,1219153,9289175,219848}
| 1
651912 | {2169145,395443,7203159,4,1483408,1120127,6826670,3833242,6593556,9610959,6037787,3663295,3832153,3011352,59413,4805726,2928469,1346520,8866551,4802519,6669386,9989045,4906640,5515378}
| 1
917170 | {5533700,8089318,3041627,7271777,8265739,1327529,8297258,4216273,4787578,7353886,3309096,1256584,2658659,9234522,8992017,3716316,8041219,434949,5098162,3389473,4639068,1073895,9440283,8107232,71786,7042329,6710428,9191641,3}
| 1
1029696 | {3265253,7656164,8567524,2652267,3168337,4980160,6712196,2,5902105,3649837,1030683,8693620,7325769,8948287,1392751,2025064}
| 1
1061817 | {1096653,3653819,9251346,6068360,8292737,603196,8884739,8447750,135140,7614256,8759570,328858,4176508,7602119,42971,5118033,3188444,2,2115724,9115069,4817618}
| 1
1134245 | {6530421,6214242,6395054,9258718,8725118,4983503,9810497,5607732,8881705,5471907,4089655,9255985,5546890,3130739,7958510,1857659,2265983,6924058,5347269,9948938,7998525,8490561,7620058,4026548,1767506,6669122,4,6825812,4389614
,4807713,3707007,920035,1021955,102061,178752,9747073,5085565,9989250,5354805,3967269,5461156,9444459,3223254,1008046,2575199,1181764,2865706} | 1
1293841 | {6304557,4210279,3,38877,1218015,3484369,3730857,2397837,1043963,1445075,8266792,3945016,5239953,8634247,3817106,8527009,1330729,7244838,1698105,8424011,2576912,8464701,9057905,9677858,5535620,914864,856093,3177092,9996328,188
841} | 1
1346505 | {9032400,4389590,650321,7262898,1704250,8295282,9849186,5449984,357623,4597835,1815568,7895683,8041120,4764576,3046330,2,8880797,7835529,6114696,4749228,7791711,4044832}
| 1
240060 | {4931779,4329891,8609630,624826,5139777,2945988,5850613,5479581,965198,8512392,9838013,5090273,721891,437386,4901686,7505060,9649984,2944743,9557274,2422698,6636513,6762844,538118,1,1727268,2164825,2070053,3387449}
| 1
(10 rows)
按相似度排序,输出10条
postgres=# explain (analyze,verbose,timing,costs,buffers)
select
*,
smlar( arr, '{1,2,3,4,5}'::int8[], 'N.i' )
from
test
where
arr % '{1,2,3,4,5}'::int8[] -- where cosine similarity >= smlar.threshold
order by
smlar( arr, '{1,2,3,4,5}'::int8[] ) desc
limit 10;
QUERY PLAN
------------------------------------------------------------------------------------------------------------------------------------------
Limit (cost=76987.64..76987.66 rows=10 width=278) (actual time=66.506..66.510 rows=10 loops=1)
Output: id, arr, (smlar(arr, '{1,2,3,4,5}'::bigint[], 'N.i'::text)), (smlar(arr, '{1,2,3,4,5}'::bigint[]))
Buffers: shared hit=3741
-> Sort (cost=76987.64..77137.64 rows=60000 width=278) (actual time=66.504..66.507 rows=10 loops=1)
Output: id, arr, (smlar(arr, '{1,2,3,4,5}'::bigint[], 'N.i'::text)), (smlar(arr, '{1,2,3,4,5}'::bigint[]))
Sort Key: (smlar(test.arr, '{1,2,3,4,5}'::bigint[])) DESC
Sort Method: top-N heapsort Memory: 28kB
Buffers: shared hit=3741
-> Bitmap Heap Scan on public.test (cost=545.60..75691.06 rows=60000 width=278) (actual time=1.743..65.204 rows=3725 loops=1)
Output: id, arr, smlar(arr, '{1,2,3,4,5}'::bigint[], 'N.i'::text), smlar(arr, '{1,2,3,4,5}'::bigint[])
Recheck Cond: (test.arr % '{1,2,3,4,5}'::bigint[])
Heap Blocks: exact=3720
Buffers: shared hit=3741
-> Bitmap Index Scan on test_arr_idx (cost=0.00..530.60 rows=60000 width=0) (actual time=1.062..1.062 rows=3725 loops=1)
Index Cond: (test.arr % '{1,2,3,4,5}'::bigint[])
Buffers: shared hit=21
Planning time: 0.102 ms
Execution time: 66.551 ms
(18 rows)
postgres=# set enable_seqscan=off;
SET
postgres=# explain (analyze,verbose,timing,costs,buffers)
select
*,
smlar( arr, '{1,2,3,4,5}'::int8[], 'N.i' )
from
test
where
arr % '{1,2,3,4,5}'::int8[] -- where cosine similarity >= smlar.threshold
limit 1;
QUERY PLAN
------------------------------------------------------------------------------------------------------------------------------------
Limit (cost=545.60..546.85 rows=1 width=274) (actual time=1.699..1.699 rows=1 loops=1)
Output: id, arr, (smlar(arr, '{1,2,3,4,5}'::bigint[], 'N.i'::text))
Buffers: shared hit=22
-> Bitmap Heap Scan on public.test (cost=545.60..75541.06 rows=60000 width=274) (actual time=1.697..1.697 rows=1 loops=1)
Output: id, arr, smlar(arr, '{1,2,3,4,5}'::bigint[], 'N.i'::text)
Recheck Cond: (test.arr % '{1,2,3,4,5}'::bigint[])
Heap Blocks: exact=1
Buffers: shared hit=22
-> Bitmap Index Scan on test_arr_idx (cost=0.00..530.60 rows=60000 width=0) (actual time=1.057..1.057 rows=3725 loops=1)
Index Cond: (test.arr % '{1,2,3,4,5}'::bigint[])
Buffers: shared hit=21
Planning time: 0.092 ms
Execution time: 1.729 ms
(13 rows)
A Generalized Inverted (GIN) index is an element expansion index. Following steps describes the GIN index optimization process:
Step 1. Creation Optimization: To accelerate index creation, set a large maintenance_work_mem value while creating a GIN index.
视实际的主机环境设置
set maintenance_work_mem='32GB';
Step 2. Update, Insertion, and Deletion Optimization: Multiple GIN entries need to be updated when an array is inserted or some records are updated or deleted. As a result, the GIN index is updated frequently. PostgreSQL designed a pending list to asynchronously update pending list information to a GIN index for reducing GIN index updates and improving data manipulation language (DML) efficiency. For more detailed information, refer to this article or read this blog
create index idx on table using gin (column,,,,,) with (fastupdate=on, gin_pending_list_limit=32767); -- pending list=32 MB
pending list会在autovacuum或者手工vacuum时合并到gin索引中
Step 3. Query Optimization: The pending list may affect query efficiency because it is not a tree structure. It is recommended that you balance the DML efficiency and query. Alternatively, if you find that the speed is slow, run the vacuum to merge the pending list to the tree.
A GIN index creates a B-tree with the product IDs as the keys. The key values are heap table line numbers (CTIDs) that compose a posting list or posting tree. When a shopping guide article is received, the database searches for B-tree keys based on product IDs involved in the shopping guide article. If a key matches a product ID, the CNT value is increased by 1. If the CNT value is smaller than the smlar.threshold value, null is returned and no next-layer search is performed. However, if the CNT value is greater than or equal to the threshold, the next-layer search is performed.
The GIN index supports the common bitmap scan search, which is completed in the following two phases:
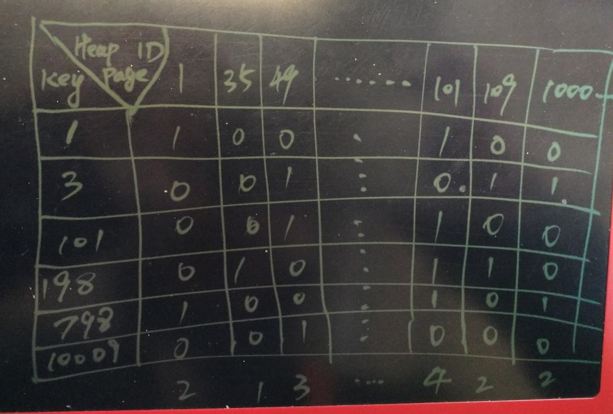
Filter heap page IDs that do not meet requirements based on smlar.threshold. For example, if smlar.threshold is 3, heap page IDs 49 and 101 meet requirements. Generate a bitmap where each bit corresponds to a heap table page. Therefore, the bitmap length depends on the number of pages in the heap table. Set bits corresponding to heap page IDs 49 and 101 that meet requirements to 1 and others to 0. This initiates the bitmap heap scan phase.
Initiate verification process by following the steps listed below.
Step 1. Set the intersection mode to overlap.
postgres=# set smlar.type='overlap';
SET
Step 2. Set the threshold to 1. Prior to the heap page bitmap generation, heap page IDs that do not meet requirements are filtered off based on the threshold.
postgres=# set smlar.threshold=1;
SET
Step 2.1. View "Heap Blocks: exact = 4011". It indicates that there are 4,011 heap page IDs that meet requirements.
postgres=# explain (analyze,verbose,timing,costs,buffers)
select
*,
smlar( arr, '{1,2,3,4,5,7262898,650321}'::int8[], 'N.i' )
from
test
where
arr % '{1,2,3,4,5,7262898,650321}'::int8[] -- where cosine similarity >= smlar.threshold
;
QUERY PLAN
------------------------------------------------------------------------------------------------------------------------------
Bitmap Heap Scan on public.test (cost=566.40..75561.86 rows=60000 width=274) (actual time=1.982..57.561 rows=4017 loops=1)
Output: id, arr, smlar(arr, '{1,2,3,4,5,7262898,650321}'::bigint[], 'N.i'::text)
// heap scan阶段,需要recheck
Recheck Cond: (test.arr % '{1,2,3,4,5,7262898,650321}'::bigint[])
// 扫描了多少heap page
Heap Blocks: exact=4011
// 扫描了多少heap page+index page
Buffers: shared hit=4040
// 以下是bitmap index scan阶段,过滤不满足条件的heap page id,生成bitmap
-> Bitmap Index Scan on test_arr_idx (cost=0.00..551.40 rows=60000 width=0) (actual time=1.282..1.282 rows=4017 loops=1)
Index Cond: (test.arr % '{1,2,3,4,5,7262898,650321}'::bigint[])
Buffers: shared hit=29
Planning time: 0.083 ms
Execution time: 57.852 ms
(10 rows)
Step 2.2. Now, set the threshold to 2 and verify as shown below.
postgres=# set smlar.threshold=2; -- 设置为2,说明 CNT[heap_page_id] >= 2
SET
postgres=# explain (analyze,verbose,timing,costs,buffers)
select
*,
smlar( arr, '{1,2,3,4,5,7262898,650321}'::int8[], 'N.i' )
from
test
where
arr % '{1,2,3,4,5,7262898,650321}'::int8[] -- where cosine similarity >= smlar.threshold
;
QUERY PLAN
---------------------------------------------------------------------------------------------------------------------------
Bitmap Heap Scan on public.test (cost=566.40..75561.86 rows=60000 width=274) (actual time=0.603..0.604 rows=1 loops=1)
Output: id, arr, smlar(arr, '{1,2,3,4,5,7262898,650321}'::bigint[], 'N.i'::text)
Recheck Cond: (test.arr % '{1,2,3,4,5,7262898,650321}'::bigint[])
// 设置了threshold=2后,只扫描了1个heap page,是不是很开心呢?
Heap Blocks: exact=1
Buffers: shared hit=30
// index scan的page不变,因为条件没有变化。但是生成的bitmap中bit=1的只有1个heap page了。
-> Bitmap Index Scan on test_arr_idx (cost=0.00..551.40 rows=60000 width=0) (actual time=0.559..0.559 rows=1 loops=1)
Index Cond: (test.arr % '{1,2,3,4,5,7262898,650321}'::bigint[])
Buffers: shared hit=29
Planning time: 0.084 ms
Execution time: 0.635 ms
(10 rows)
Step 2.3 The following commands provide another example.
postgres=# set smlar.threshold=3;
SET
postgres=# explain (analyze,verbose,timing,costs,buffers)
select
*,
smlar( arr, '{1,2,3,4,5,7262898,650321}'::int8[], 'N.i' )
from
test
where
arr % '{1,2,3,4,5,7262898,650321}'::int8[] -- where cosine similarity >= smlar.threshold
;
QUERY PLAN
---------------------------------------------------------------------------------------------------------------------------
Bitmap Heap Scan on public.test (cost=566.40..75561.86 rows=60000 width=274) (actual time=0.495..0.496 rows=1 loops=1)
Output: id, arr, smlar(arr, '{1,2,3,4,5,7262898,650321}'::bigint[], 'N.i'::text)
Recheck Cond: (test.arr % '{1,2,3,4,5,7262898,650321}'::bigint[])
Heap Blocks: exact=1
Buffers: shared hit=30
-> Bitmap Index Scan on test_arr_idx (cost=0.00..551.40 rows=60000 width=0) (actual time=0.452..0.452 rows=1 loops=1)
Index Cond: (test.arr % '{1,2,3,4,5,7262898,650321}'::bigint[])
Buffers: shared hit=29
Planning time: 0.083 ms
Execution time: 0.526 ms
(10 rows)
Step 2.4 Now, when the threshold is 4, no bit in the bitmap is set to 1 in the bitmap index scan phase. Therefore, in the bitmap heap scan phase, the number of scanned pages is 0.
postgres=# set smlar.threshold=4;
SET
postgres=# explain (analyze,verbose,timing,costs,buffers)
select
*,
smlar( arr, '{1,2,3,4,5,7262898,650321}'::int8[], 'N.i' )
from
test
where
arr % '{1,2,3,4,5,7262898,650321}'::int8[] -- where cosine similarity >= smlar.threshold
;
QUERY PLAN
---------------------------------------------------------------------------------------------------------------------------
Bitmap Heap Scan on public.test (cost=566.40..75561.86 rows=60000 width=274) (actual time=0.370..0.370 rows=0 loops=1)
Output: id, arr, smlar(arr, '{1,2,3,4,5,7262898,650321}'::bigint[], 'N.i'::text)
Recheck Cond: (test.arr % '{1,2,3,4,5,7262898,650321}'::bigint[])
Buffers: shared hit=29
-> Bitmap Index Scan on test_arr_idx (cost=0.00..551.40 rows=60000 width=0) (actual time=0.368..0.368 rows=0 loops=1)
Index Cond: (test.arr % '{1,2,3,4,5,7262898,650321}'::bigint[])
Buffers: shared hit=29
Planning time: 0.083 ms
Execution time: 0.404 ms
(9 rows)
It is simple to query the CTID or heap page ID.
postgres=# set smlar.threshold=1;
SET
postgres=# select
ctid, -- 行号
split_part(ctid::text, ',', 1) -- heap page id
from
test
where
arr % '{1,2,3,4,5,7262898,650321}'::int8[] -- where cosine similarity >= smlar.threshold
;
ctid | split_part
--------------+------------
(1165,10) | (1165
(1487,6) | (1487
(9038,12) | (9038
(9300,15) | (9300
(13926,18) | (13926
(22472,24) | (22472
......
The efficiency is verified before. If there are 60 million shopping guide articles (including 50 million for common products and 10 million for hot products) and 40 products (including 5 hot products and 35 common products), the TPS for real-time similarity determination is 10,000.
The GIN and GiST implementations of the smlar plug-in will be introduced later.
Build your own PostgreSQL solution on Alibaba Cloud with ApsaraDB for RDS PostgreSQL.
Similarity Algorithms: Effective Similarity Search in PostgreSQL
Alibaba Cloud Community - September 5, 2024
Alibaba EMR - January 10, 2023
Alibaba Cloud MaxCompute - October 18, 2021
Kaiwai - September 9, 2019
Alibaba Cloud MaxCompute - October 18, 2021
XianYu Tech - March 11, 2020
 PolarDB for PostgreSQL
PolarDB for PostgreSQL
Alibaba Cloud PolarDB for PostgreSQL is an in-house relational database service 100% compatible with PostgreSQL and highly compatible with the Oracle syntax.
Learn More AnalyticDB for PostgreSQL
AnalyticDB for PostgreSQL
An online MPP warehousing service based on the Greenplum Database open source program
Learn More Vector Retrieval Service for Milvus
Vector Retrieval Service for Milvus
A cloud-native vector search engine that is 100% compatible with open-source Milvus, extensively optimized in performance, stability, availability, and management capabilities.
Learn More Livestreaming for E-Commerce Solution
Livestreaming for E-Commerce Solution
Set up an all-in-one live shopping platform quickly and simply and bring the in-person shopping experience to online audiences through a fast and reliable global network
Learn MoreMore Posts by digoal