This section considers the most classic diet (Diet) problem in mathematical programming.
There are eight foods in the recipe: beef (BEEF), chicken (CHK), fish (FISH), ham (HAM), macaroni with cheese (MCH), meatloaf (MTL), pasta (SPG), turkey (TUR). At the same time, there are four vitamins people consume every day: A, C, B1, and B.
The vitamin content per gram of food is shown in the following figure:
| Vitamin A | Vitamin C | Vitamin B1 | Vitamin B2 | |
| BEEF | 60 | 20 | 10 | 15 |
| CHK | 8 | 0 | 20 | 20 |
| FISH | 8 | 10 | 15 | 10 |
| HAM | 0 | 40 | 35 | 10 |
| MCH | 15 | 35 | 0 | 15 |
| MTL | 70 | 30 | 15 | 0 |
| SPG | 0 | 50 | 25 | 15 |
| TUR | 60 | 0 | 15 | 0 |
The cost per gram of food is below:
| Price per gram | |
| BEEF | 3.19 yuan/g |
| CHK | 2.59 yuan/g |
| FISH | 2.29 yuan/g |
| HAM | 2.89 yuan/g |
| MCH | 1.89 yuan/g |
| MTL | 1.99 yuan/g |
| SPG | 1.99 yuan/g |
| TUR | 2.49 yuan/g |
Suppose the intake of each food should not exceed 100 grams per person per day, and the intake of each vitamin should not be less than 700 but not more than 10000. How do we make food intake decisions to minimize the amount of money we spend on food while meeting the requirements above?
The mathematical model of the problem above is listed below:
xj ∈[fmin,j, fmax,j] is someone's daily intake of food j∈F.
Minimize food total cost:
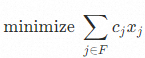
The intake per person for nutrition i∈N is between minimum nmin,i and maximum nmax,i :
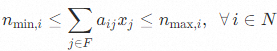
Next, open a notebook with MAPL kernel.
In order to open a new notebook with MAPL as the kernel, click the + button in the top left corner of the platform to open the launcher. This will also create a .ipynb file. In this tutorial, the file is named 01_HowToEat_diet.ipynb. The kernel of the notebook can be switched in the top right corner of the editor.
Then, create a new code cell and input the code from the next cell below. Please note that each command should end with a semicolon.
In order to run the cell, click the triangle button above the window or press the Ctrl + Enter or Shift + Enter keys.
clear model; #Used when running multiple times to clear the model
option modelname model/diet; #Facilitate the generation of intermediate files in the same directory as Method 2.
print "-----------------Modeling---------------";
#--------------------------
# diet.mapl
# The data in this example is《AMPL: A Modeling Language for Mathematical Programming》chapter Two the example of diet is adapted
set NUTR := { "A", "B1", "B2", "C" };
set FOOD := {"BEEF", "CHK", "FISH", "HAM", "MCH", "MTL", "SPG", "TUR"} ;
set F:= {"cost", "f_min", "f_max"};
set N:= {"n_min", "n_max"};
param data1[FOOD * F] :=
| "cost" , "f_min" , "f_max" |
|"BEEF" | 3.19 , 0 , 100 |
|"CHK" | 2.59 , 0 , 100 |
|"FISH" | 2.29 , 0 , 100 |
|"HAM" | 2.89 , 0 , 100 |
|"MCH" | 1.89 , 0 , 100 |
|"MTL" | 1.99 , 0 , 100 |
|"SPG" | 1.99 , 0 , 100 |
|"TUR" | 2.49 , 0 , 100 |;
param data2[NUTR * N] :=
| "n_min", "n_max"|
|"A" | 700, 10000 |
|"C" | 700, 10000 |
|"B1" | 700, 10000 |
|"B2" | 700, 10000 |;
param amt[FOOD * NUTR] :=
| "A", "C", "B1", "B2"|
|"BEEF" | 60, 20, 10, 15 |
|"CHK" | 8, 0, 20, 20 |
|"FISH" | 8, 10, 15, 10 |
|"HAM" | 0, 40, 35, 10 |
|"MCH" | 15, 35, 0, 15 |
|"MTL" | 70, 30, 15, 0 |
|"SPG" | 0, 50, 25, 15 |
|"TUR" | 60, 0, 15, 0 |;
var x[j in FOOD] >= data1[j, "f_min"] <= data1[j, "f_max"];
minimize Total_Cost: sum {j in FOOD} : data1[j, "cost"] * x[j];
subto Diet: forall {i in NUTR}
data2[i, "n_min"] <= sum {j in FOOD}: amt[j, i] * x[j] <= data2[i, "n_max"];
#------------------------------
print "-----------------Solving using MindOpt---------------";
option solver mindopt; # (Optional) Specify the solver for solving, the default is MindOpt
solve;
print "-----------------Display---------------";
display; # Show Results
print "The lowest price is:";
print sum {<j> in FOOD} data1[j, "cost"] * x[j];We can save the modeling part codes in file diet.mapl and call MAPL to load the file.
*diet.mapl diet.nl and diet.sol file can be viewed in MindOpt Studio diet plan cases.
clear model; #Used when running multiple times to clear the model
print "-----------------Modeling---------------";
model model/diet.mapl;
print "-----------------Solving using MindOpt---------------";
option solver mindopt; # (Optional) Specify the solver for solving, the default is MindOpt
solve;
print "-----------------Display---------------";
display; # Show Results
print "The lowest price is:";
print sum {<j> in FOOD} data1[j, "cost"] * x[j];The results of Method 1 and Method 2 are consistent:
-----------------Modeling---------------
-----------------Solving using MindOpt---------------
Running mindoptampl
wantsol=1
mip_integer_tolerance=1e-9
MindOpt Version 0.24.1 (Build date: 20230423)
Copyright (c) 2020-2023 Alibaba Cloud.
Start license validation (current time : 13-JUN-2023 20:42:45).
License validation terminated. Time : 0.002s
Only one thread allowed -- optimize with Simplex method.
Model summary.
- Num. variables : 8
- Num. constraints : 4
- Num. nonzeros : 25
- Bound range : [1.0e+02,1.0e+04]
- Objective range : [1.9e+00,3.2e+00]
- Matrix range : [8.0e+00,7.0e+01]
Presolver started.
Presolver terminated. Time : 0.000s
Simplex method started.
Model fingerprint: iVWY5d2diV2dvd3Y
Iteration Objective Dual Inf. Primal Inf. Time
0 0.00000e+00 0.0000e+00 2.6250e+02 0.00s
4 1.01011e+02 0.0000e+00 0.0000e+00 0.00s
Postsolver started.
Simplex method terminated. Time : 0.002s
OPTIMAL; objective 101.01
4 simplex iterations
Completed.
-----------------Display---------------
Primal Solution:
x@BEEF = 0.000000000000000E+00
x@CHK = 2.497123130034522E+01
x@FISH = 0.000000000000000E+00
x@HAM = 0.000000000000000E+00
x@MCH = 8.538550057537401E+00
x@MTL = 5.316455696202531E+00
x@SPG = 4.833141542002300E+00
x@TUR = 0.000000000000000E+00
Dual Solution:
Diet_1 = 2.438506904487917E-02
Diet_2 = 1.852876869965478E-02
Diet_3 = 1.012172036823936E-01
Diet_4 = 1.704545454545448E-04
The lowest price is:
101.0110471806674After executing the command above, we use display to get the following output:
Primal Solution:
x@BEEF = 0.000000000000000E+00
x@CHK = 2.497123130034522E+01
x@FISH = 0.000000000000000E+00
x@HAM = 0.000000000000000E+00
x@MCH = 8.538550057537401E+00
x@MTL = 5.316455696202531E+00
x@SPG = 4.833141542002300E+00
x@TUR = 0.000000000000000E+00
x@TUR = 0.000000000000000E+00
Dual Solution:
Diet_1 = 2.438506904487917E-02
Diet_2 = 1.852876869965478E-02
Diet_3 = 1.012172036823936E-01
Diet_4 = 1.704545454545448E-04
The lowest price is:
101.0110471806674Print x@name is the value of the decision variable, followed by the dual solution.
At the same time, the corresponding diet.nl and diet.sol file will be generated at the folder option modelname defined.
The .nl file is the programming problem model file, which can be recognized by most solvers, and the solution result solution is stored in the .sol file.
The practical meaning of the solution for this problem represents the recommended foods – chicken (CHK), macaroni cheese (MCH), meatloaf (MTL), and pasta (SPG).
MindOpt - August 24, 2023
MindOpt - August 29, 2023
MindOpt - August 29, 2023
MindOpt - August 29, 2023
Alibaba Cloud Community - September 19, 2024
Alibaba Cloud Community - April 11, 2023
Alibaba Cloud Academy
Alibaba Cloud provides beginners and programmers with online course about cloud computing and big data certification including machine learning, Devops, big data analysis and networking.
Learn More
CloudBox
Fully managed, locally deployed Alibaba Cloud infrastructure and services with consistent user experience and management APIs with Alibaba Cloud public cloud.
Learn More
Alibaba Cloud Flow
An enterprise-level continuous delivery tool.
Learn More